Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





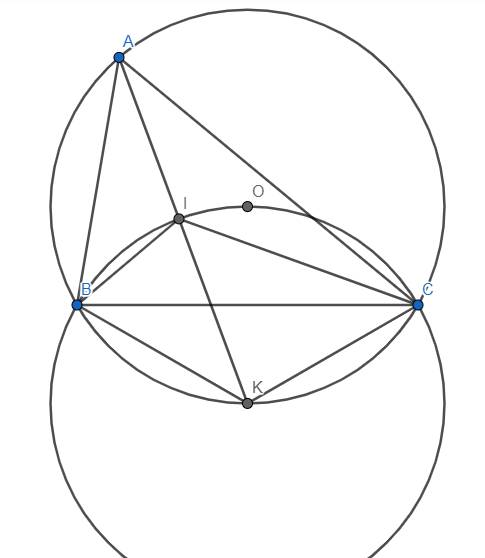
Gọi (O) là đường tròn ngoại tiếp tam giác ABC, AI cắt (O) tại K. Theo bổ đề quen thuộc thì K là tâm của (BIC). Hơn nữa \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=120^o\) và \(\widehat{BOC}=2\widehat{BAC}=120^o\) nên \(\widehat{BIC}=\widehat{BOC}\), suy ra tứ giác BIOC nội tiếp, suy ra \(O\in\left(K\right)\). Điều này có nghĩa bán kính của \(\left(K\right)\) chính là \(OK=2\).

`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)

7.
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm \(I=\left(a;b\right)\), bán kính \(R\)
\(\Rightarrow\) Tâm đường tròn \(\left(x-1\right)^2+\left(y+2\right)^2=4\) có tọa độ \(\left(1;-2\right)\)
Kết luận: Tâm đường tròn có tọa độ \(\left(1;-2\right)\).

11:

a: ABCD là hình chữ nhật
=>vecto AB+vecto AD=vecto AC
\(AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a\)
b: Gọi M là trung điểm của BC
=>BM=MC=4a/2=2a
Trên tia đối của tia MA lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}=2\cdot\overrightarrow{AM}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{\left(3a\right)^2+\left(2a\right)^2}=a\sqrt{13}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)



 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn