Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
-Kiểu 1: \(S=\dfrac{1}{2}\cdot130\cdot120=7800\left(cm^2\right)\)
\(V=7800\cdot250=1950000\left(cm^3\right)\)
-Kiểu 2: \(S=\dfrac{1}{2}\cdot120\cdot120=7200\left(cm^2\right)\)
\(V=7200\cdot260=1872000\left(cm^3\right)\)
-Kiểu 3: \(S=\dfrac{1}{2}\cdot150\cdot116=8700\left(cm^2\right)\)
\(V=8700\cdot232=2018400\left(cm^3\right)\)
b:
-Kiểu 1:
Diện tích hai mặt bên là:
\(2\cdot136\cdot250=68000\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
7800+68000=75800(cm2)
-Kiểu 2:
DIện tích hai mặt bên là:
\(2\cdot134\cdot260=69680\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là;
\(7200+69680=76880\left(cm^2\right)\)
-Kiểu 3:
Diện tích hai mặt bên là:
\(2\cdot137\cdot232=63568\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
\(63568+8700=72268\left(cm^2\right)\)
c: Chọn kiều lều 3 vì thể tích lớn nhất

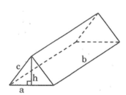
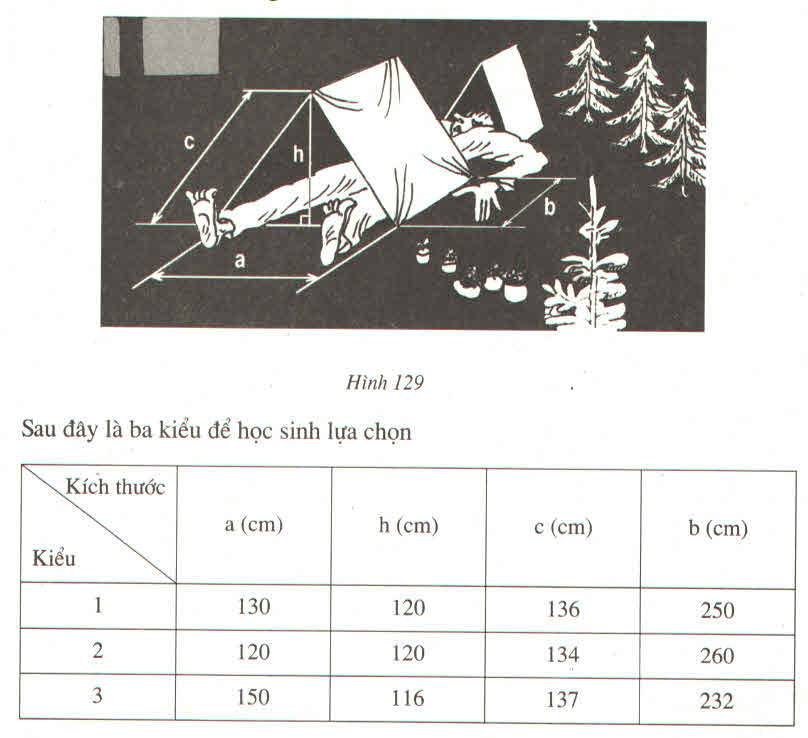
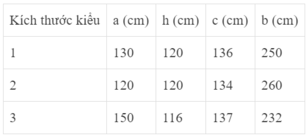
Ta có thể xem cái lều là một làng trụ đứng đáy tam giác cân cạnh bên bằng c, cạnh đáy bằng a, đường cao đáy là h, đường cao hình lăng trụ là b.
Áp dụng công thức: V = S.h, ta có:
*Kiểu 1: S=1/2 .130.120= 7800 ( c m 2 )
V = 7800.250 =1950000 ( c m 3 )
*Kiểu 2: S =1/2 .120.120 = 7200 ( c m 2 )
V = 7200.260= 1872000 ( c m 3 )
Kiểu 3: S=1/2 .150.116=8700 ( c m 2 )
V = 8700.232 = 2018400 ( c m 3 )

S A B x x x x 20 cm
Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2
Thể tích Trái đất bằng 1,0832073×1012 km3
Thể tích hình cầu bằng \(\frac{4}{3}\)pi . r3 (r là bán kính hình cầu)
Số pi làm tròn là 3,14
Thể tích 1,0832073×1012 km3