
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1+\sqrt{2}\\x\le-1-\sqrt{2}\end{matrix}\right.\)
\(x^2-2x-1+2\left(x-1\right)\sqrt{x^2+2x-1}=0\)
\(\Leftrightarrow\left(x^2+2x-1\right)+2\left(x-1\right)\sqrt{x^2+2x-1}-4x=0\)
\(\Delta'=\left(x-1\right)^2+4x=\left(x+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=1-x+x+1\\\sqrt{x^2+2x-1}=1-x-x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=2\\\sqrt{x^2+2x-1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+2x-1=4\\x^2+2x-1=4x^2\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow x\)
b.
ĐKXĐ: \(x\ge-\sqrt[3]{3}\)
\(x^3+3-\left(5x-1\right)\sqrt{x^3+3}+6x^2-2x=0\)
Đặt \(\sqrt{x^3+3}=t\ge0\)
\(\Rightarrow t^2-\left(5x-1\right)t+6x^2-2x=0\)
\(\Delta=\left(5x-1\right)^2-4\left(6x^2-2x\right)=\left(x-1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{5x-1-x+1}{2}=2x\\t=\dfrac{5x-1+x-1}{2}=3x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^3+3}=2x\left(x\ge0\right)\\\sqrt{x^3+3}=3x-1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^3+2=4x^2\left(x\ge0\right)\\x^3+3=9x^2-6x+1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x^2-3x-3\right)=0\left(x\ge0\right)\\\left(x-1\right)\left(x^2-8x-2\right)=0\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)

a: \(=3-2\sqrt{2}+3+2\sqrt{2}=6\)
b: \(=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}=-2\sqrt{2}\)
\(a,=3-2\sqrt{2}+3+2\sqrt{2}=6\\ b,=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\\ c,=2-\sqrt{3}+\sqrt{3}-1=1\\ d,=3+\sqrt{2}-\sqrt{2}+1=4\\ e,=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}=-2\sqrt{2}\\ f,=\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\\ g,=\sqrt{\left(2+2\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}=2+2\sqrt{5}+\sqrt{5}-2=3\sqrt{5}-4\left(đáp.số.đã.cho.sai\right)\\ h,=\sqrt{\left(3-2\sqrt{2}\right)^2}+\sqrt{\left(2\sqrt{2}+1\right)^2}=3-2\sqrt{2}+2\sqrt{2}+1=4\)

\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)

Bài 1:
Gọi vận tốc và thời gian dự định là a,b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(a+3\right)\left(b-2\right)=ab\\\left(a-3\right)\left(b+3\right)=ab\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+3b=6\\3a-3b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=15\\b=6\end{matrix}\right.\)
Vậy: Chiều dài khúc sông là 90km

1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17


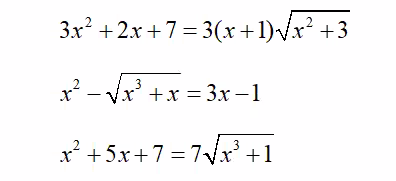
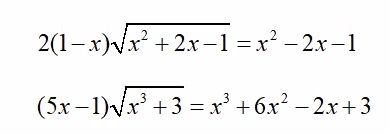


 mn giúp em với em cần gấp bài 2 nha thank you
mn giúp em với em cần gấp bài 2 nha thank you 


a.
\(\Leftrightarrow\left(x+1\right)^2+2\left(x^2+3\right)=3\left(x+1\right)\sqrt{x^2+3}\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{x^2+3}=b\end{matrix}\right.\) ta được:
\(a^2+2b^2=3ab\)
\(\Leftrightarrow\left(a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=2b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+3}=x+1\\2\sqrt{x^2+3}=x+1\end{matrix}\right.\) (\(x\ge-1\))
\(\Rightarrow\left[{}\begin{matrix}x^2+3=x^2+2x+1\\4\left(x^2+3\right)=x^2+2x+1\end{matrix}\right.\) (\(x\ge-1\))
\(\Rightarrow...\)
b.
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow x^2+1-\sqrt{x\left(x^2+1\right)}-3x=0\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+1}=a>0\\\sqrt{x}=b\ge0\end{matrix}\right.\)
\(\Rightarrow a^2-ab-3b^2=0\) (đề cho hệ số không hợp lý chút xíu nào)
\(\Leftrightarrow\left(a-\dfrac{1+\sqrt{13}}{2}b\right)\left(a+\dfrac{\sqrt{13}-1}{2}b\right)=0\)
\(\Leftrightarrow a=\dfrac{1+\sqrt{13}}{2}b\)
\(\Leftrightarrow\sqrt{x^2+1}=\dfrac{1+\sqrt{13}}{2}\sqrt{x}\)
\(\Leftrightarrow x^2+1=\dfrac{7+\sqrt{13}}{2}x\)
\(\Leftrightarrow x^2-\dfrac{7+\sqrt{13}}{2}x+1=0\)
Tới đây em chịu khó tính delta bằng tay rồi tính nghiệm