CV
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
7
PT
1
CM
15 tháng 4 2017
- Định lí Py – ta – go thuận:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Định lí Py – ta – go đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
PT
1
CM
28 tháng 8 2017
- Định lí Py – ta – go thuận:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Định lí Py – ta – go đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
ID
6
8 tháng 2 2018
Định lý Pytago đã được biết đến từ lâu trước thời của Pythagoras, nhưng ông được coi là người đầu tiên nêu ra chứng minh định lý này.[2] Cách chứng minh của ông rất đơn giản, chỉ bằng cách sắp xếp lại hình vẽ.
Trong hai hình vuông lớn ở hình minh họa bên trái, mỗi hình vuông chứa bốn tam giác vuông bằng nhau, sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pytago, Q.E.D.[9]
Về sau, trong tác phẩm của nhà triết học và toán học Hy Lạp Proclus đã dẫn lại chứng minh rất đơn giản của Pythagoras.[10] Các đoạn dưới đây nêu ra một vài cách chứng minh khác, nhưng cách chứng minh ở trên thuộc về của Pythagoras.
Những dạng khác của định lý[sửa | sửa mã nguồn]
Như đã nhắc đến ở đoạn giới thiệu, nếu c ký hiệu là chiều dài của cạnh huyền và a và b ký hiệu là chiều dài của hai cạnh kề, định lý Pytago có thể biểu diễn bằng phương trình Pytago:
{\displaystyle a^{2}+b^{2}=c^{2}.}
Nếu đã biết chiều dài cả a và b, thì cạnh huyền c tính bằng
{\displaystyle c={\sqrt {a^{2}+b^{2}}}.}
Nếu biết độ dài của cạnh huyền c và một trong các cạnh kề (a hoặc b), thì độ dài của cạnh kề còn lại được tìm bằng công thức: {\displaystyle a={\sqrt {c^{2}-b^{2}}}}
{\displaystyle b={\sqrt {c^{2}-a^{2}}}.}
Phương trình Pytago cho liên hệ các cạnh của một tam giác vuông theo cách đơn giản, do đó nếu biếu chiều dài của hai cạnh bất kỳ thì sẽ tìm được chiều dài của cạnh còn lại. Một hệ quả khác của định lý đó là trong bất kỳ tam giác vuông nào, cạnh huyền luôn lớn hơn hai cạnh kia, nhưng bé hơn tổng của hai cạnh.
Định lý khái quát định lý này cho tam giác bất kỳ này đó là định lý cos, cho phép tính chiều dài của một cạnh khi biết chiều dài của hai cạnh kia cũng như góc tạo bởi hai cạnh này. Nếu góc giữa hai cạnh này là góc vuông, định lý cos sẽ trở về trường hợp đặc biệt đó là định lý Pytago.
Các chứng minh khác[sửa | sửa mã nguồn]
Định lý này có thể coi là định lý có nhiều cách chứng minh nhất (luật tương hỗ bậc hai là một định lý khác có nhiều cách chứng minh); trong cuốn sách The Pythagorean Proposition nêu ra 370 cách chứng minh cho định lý Pytago.[11]
Chứng minh sử dụng các tam giác đồng dạng[sửa | sửa mã nguồn]
Chứng minh sử dụng các tam giác đồng dạng.
Chứng minh này dựa trên sự tỉ lệ thuận của các cạnh của hai tam giác đồng dạng, tức là nó dựa trên tỉ số của hai cạnh tương ứng của hai tam giác đồng dạng là như nhau với kích thước của tam giác là bất kỳ.
Gọi ABC là một tam giác vuông, với góc vuông nằm tại đỉnh C, như ở hình bên. Vẽ đường cao tam giác từ điểm C, và gọi H là chân đường cao nằm trên cạnh AB. Điểm H chia chiều dài cạnh huyền c thành hai đoạn AH và BH. Tam giác mới ACH đồng dạng với tam ABC, bởi vì chúng đều có góc vuông (như theo định nghĩa của đường cao), và có chung góc tại đỉnh A, điều này có nghĩa rằng góc thứ ba còn lại cũng bằng nhau, ký hiệu θ như trong hình. Lập luận tương tự, tam giác CBH cũng đồng dạng với tam giác ABC. Chứng minh hai tam giác đồng dạng dựa trên mệnh đề về các góc trong tam giác: tổng các góc trong một tam giác bằng hai lần góc vuông, và tương đương với tiên đề về hai đường thẳng song song. Hai tam giác đồng dạng cho tỉ số của các cạnh tương ứng là bằng nhau:
{\displaystyle {\frac {BC}{AB}}={\frac {BH}{BC}}{\text{ and }}{\frac {AC}{AB}}={\frac {AH}{AC}}.}
Tỉ số thứ nhất bằng cosine của góc θ, và tỉ số thứ hai bằng sin của góc này.
Viết lại các tỉ số này
{\displaystyle BC^{2}=AB\times BH{\text{ and }}AC^{2}=AB\times AH.}
Cộng hai vế của hai đẳng thức
{\displaystyle BC^{2}+AC^{2}=AB\times BH+AB\times AH=AB\times (AH+BH)=AB^{2},}
và cuối cùng thu được định lý Pytago:
{\displaystyle BC^{2}+AC^{2}=AB^{2}}
Có nhiều tranh luận xung quanh vai trò của chứng minh này trong lịch sử toán học. Câu hỏi đặt ra là tại sao Euclid đã không sử dụng chứng minh này mà ông đã nghĩ ra một cách khác. Một phỏng đoán cho rằng cách chứng minh sử dụng các tam giác đồng dạng bao gồm định lý về tỉ lệ, một chủ đề không được thảo luận cho đến tận khi ông viết cuốn Cơ sở (Elements), và định lý tỉ lệ cần được phát triển thêm ở thời điểm đó.[12][13]
Chứng minh của Euclid[sửa | sửa mã nguồn]
Chứng minh đưa ra trong cuốn Elements của Euclid.
Tóm tắt nội dung chứng minh của Euclid nêu ra trong cuốn Elements. Hình vuông lớn (có cạnh là cạnh huyền) được chia thành hai hình chữ nhật bên trái và phải (xem hình). Dựng một tam giác có diện tích bằng một nửa diện tích của hình chữ nhật bên trái. Sau đó dựng tam giác khác có diện tích bằng một nửa hình vuông ở cạnh bên trái. Bước tiếp theo là chứng minh hai tam giác này These bằng nhau, và do đó diện tích hình vuông bên trái bằng diện tích hình chữ nhật bên trái. Lập luận tương tự cho hình vuông bên phải và hình chữ nhật bên phải. Tổng diện tích hai hình chữ nhật bằng diện tích hình vuông có cạnh là cạnh huyền, và chính bằng tổng diện tích của hai hình vuông dựng trên hai cạnh kề. Chi tiết chứng minh như sau.
Gọi A, B, C là các đỉnh của một tam giác vuông, với góc vuông tại A. Hạ một đường thẳng từ A vuông góc với cạnh huyền. Đường thẳng này chia hình vuông dựng trên cạnh huyền làm hai hình chữ nhật, mà sẽ chứng minh là hai hình chữ nhật này lần lượt bằng diện tích với hai hình vuông trên hai cạnh góc vuông.
Để chứng minh chặt chẽ, đòi hỏi dựa trên bốn bổ đề cơ bản sau:
- Nếu hai tam giác có hai cạnh tương ứng bằng nhau, và góc giữa hai cạnh này cũng bằng nhau, thì hai tam giác này bằng nhau (trường hợp cạnh-góc-cạnh).
- Diện tích tam giác bằng một nửa diện tích của hình bình hành có cùng đáy và chiều cao.
- Diện tích của hình chữ nhật bằng tích của hai cạnh kề nhau.
- Diện tích của hình vuông bằng bình phương cạnh của nó (hệ quả từ bổ đề 3).
Tiếp theo, mỗi hình vuông trên từng cạnh kề được liên hệ với một tam giác tương đẳng với nó, mà tam giác này lại có liên hệ tương đẳng với một hình chữ nhật vừa chia.[14]
Minh họa chia hình vuông và dựng thêm đường.
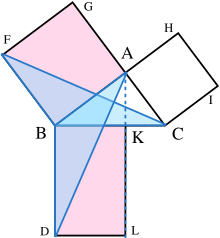
Chứng minh hai tam giác bằng nhau và chúng lần lượt bằng một nửa diện tích hình chữ nhật BDLK và hình vuông BAGF.
Chứng minh như sau:
- Gọi ABC là tam giác vuông với góc vuông CAB.
- Trên mỗi cạnh BC, AB, và CA, dựng ra các hình vuông tương ứng CBDE, BAGF, và ACIH. Việc dựng các hình vuông cũng đòi hỏi trực tiếp các định lý trước đó nêu ra trong cuốn sách của Euclid, và chỉ phụ thuộc vào tiên đề đường thẳng song song.[15]
- Từ đỉnh A, vẽ một đường thẳng song song với hai cạnh BD và CE. Nó sẽ vuông góc với BC và DE và cắt tại các điểm tương ứng K và L.
- Nối CF và AD, để tạo thành hai tam giác BCF và BDA.
- Góc CAB và BAG đều là các góc vuông; do đó các điểm C, A, và G nằm trên cùng một đường thẳng. Tương tự đối với các điểm B, A, và H.
- Góc CBD và FBA đều là các góc vuông; suy ra góc ABD bằng góc FBC, do cả hai đều bằng tổng của một góc vuông với góc ABC.
- Vì AB bằng FB và BD bằng BC, do đó hai tam giác ABD và FBC bằng nhau.
- Vì A-K-L là đường thẳng song song với cạnh BD, do đó hình chữ nhật BDLK có diện tích bằng hai lần diện tích tam giác ABD bởi vì chúng có chung cạnh đáy BD và cùng đường cao BK, đường vuông góc với cạnh đáy và nối hai đường thằng song song BD và AL. (bổ đề 2)
- Do C nằm trên cùng đường thẳng với A và G, nên hình vuông BAGF có diện tích bằng hai lần diện tích ta...
22 tháng 2 2018
Trong toán học, định lý Pytago (còn gọi là định lý Pythagore theo tiếng Anh) là một liên hệ căn bản trong hình học Euclid giữa bacạnh tam giác của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. Định lý có thể viết thành một phương trình liên hệ độ dài của các cạnh là a, b và c, thường gọi là "công thức Pytago":[1]
{\displaystyle a^{2}+b^{2}=c^{2},}
với c là độ dài cạnh huyền và a và b là độ dài hai cạnh góc vuông hay còn gọi là cạnh kề.
Mặc dù những hiểu biết về mối liên hệ này đã được biết trước thời của ông,[2][3] định lý được đặt tên theo nhà toán học Hy Lạp cổ đại Pythagoras (k. 570–495 BC) khi - với những tư liệu lịch sử đã ghi lại - ông được coi là người đầu tiên chứng minh được định lý này.[4][5][6] Có một số chứng cứ cho thấy các nhà toán học Babylon đã hiểu về công thức này, mặc dù có ít tư liệu cho thấy họ đã sử dụng nó trong khuôn khổ của toán học.[7][8] Các nhà toán học khu vực Lưỡng Hà, Ấn Độ và Trung Quốc cũng đều tự khám phá ra định lý này và trong một số nơi, họ đã đưa ra chứng minh cho một vài trường hợp đặc biệt.
Có rất nhiều chứng minh cho định lý này - và có lẽ là nhiều nhất trong các định lý của toán học. Cách chứng minh rất đa dạng, bao gồm cả chứng minh bằng hình học lẫn đại số, mà một số có lịch sử hàng nghìn năm tuổi. Định lý Pytago còn được tổng quát hóa bằng nhiều cách khác nhau, bao gồm cho không gian nhiều chiều, cho các không gian phi Euclid, cho các tam giác bất kỳ, và thậm chí cho những đối tượng khác xa hẳn so với tam giác vuông, những đối tượng hình học tổng quát trong không gian n-chiều. Định lý Pytago còn thu hút nhiều sự chú ý từ bên ngoài phạm vi toán học, như là một biểu tượng toán học thâm thúy, bí ẩn, hay sức mạnh của trí tuệ; nó cũng được nhắc tới trong văn học, kịch bản, âm nhạc, bài hát, con tem và phim hoạt hình.
HK
3
CV
10 tháng 1 2018
- cho tam giác ABC vuông tại C. Từ trung điểm K của BC, kẻ KI vuông góc với BC. CMR: \(AI^2-BI^2=AC^2\)
- cho tam giác nhọn ABC, kẻ AH vuông góc với BC. Tính chu vi của tam giác ABC biết AB= 10cm; AH= 8cm; HC= 15cm
LQ
3
NH
29 tháng 11 2016
có sai đề không bạn?
phải là \(\left(a+b\right)\left(a-b\right)=a^2-b^2\)chứ bạn?
29 tháng 11 2016
\(\left(a+b\right)\left(a-b\right)\)
\(=a^2-ab+ab-b^2\)
\(=a^2-b^2\)
CM
23 tháng 9 2017
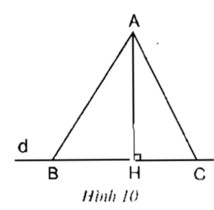
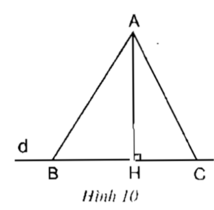
AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC
CM
25 tháng 10 2019
Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC
Định lý này được đặt tên theo nhà vật lí học và nhà toán học Hy Lạp Pytago
la py ta go