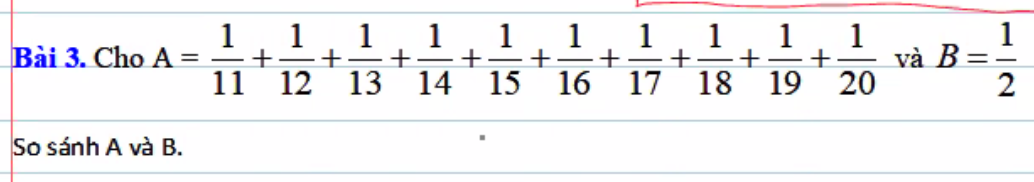Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
Ta có các phân số 1/11 ; 1/12 ; 1/13 ; 1/14 ; 1/15 ; 1/16 ; 1/17 ; 1/18 ; 1/19 đều lớn hơn 1/20
Do đó : 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16 + 1/17 + 1/18 + 1/19 + 1/20 > 1/20 + 1/20 + ;...+ 1/20 ( có 10 phân số 1/20 )
1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1 /16 + 1/17 + 1/18 + 1/19 + 1/20 > 10/20
1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1 /16 + 1/17 + 1/18 + 1/19 + 1/20 > 1/2
Vậy : S > 1/2
Ta có: \(\dfrac{1}{2}=\dfrac{10}{20}=\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\) ( Có 10 số \(\dfrac{1}{20}\) )
Mà \(\dfrac{1}{20}< \dfrac{1}{19}:\dfrac{1}{20}< \dfrac{1}{18}:...:\dfrac{1}{20}< \dfrac{1}{11}\)
\(\Rightarrow\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}< \dfrac{1}{20}+\dfrac{1}{19}+\dfrac{1}{18}+...+\dfrac{1}{11}\)
\(\Rightarrow A=B\)



Ta có : \(12a+7b=64\)
Do \(64⋮4,12a⋮4\) \(\Rightarrow7b⋮4\) mà \(\left(7,4\right)=1\)
\(\Rightarrow b⋮4\) (1)
Từ giả thiết \(\Rightarrow7b\le64\) \(\Leftrightarrow b\le9\) kết hợp với (1)
\(\Rightarrow b\in\left\{4,8\right\}\)
+) Với \(b=4\) thì : \(12a+7\cdot4=64\)
\(\Leftrightarrow12a=36\)
\(\Leftrightarrow a=3\) ( thỏa mãn )
+) Với \(b=8\) thì \(12a+7\cdot8=64\)
\(\Leftrightarrow12a=8\)
\(\Leftrightarrow a=\frac{8}{12}\) ( loại )
Vậy : \(\left(a,b\right)=\left(3,4\right)\)

\(M=896+892+888+...+24\)
\(M=\frac{\left(896+24\right).219}{2}=100740\)
\(N=18.21+21+21.79\)
\(N=21.\left(18+1+79\right)=21.100\)
\(N=2100\)
b,
N=18x21+21+21x79
N=18x21+21x1+21x79
N=(18+1+79)x21
N=98x21
N=2058

Bài 5:
a: AC+CB=AB
mà A,B,C thẳng hàng
nên C nằm giữa A và B
b: AB+BC=AC
mà A,B,C thẳng hàng
nên B nằm giữa A và C
c: BA+AC=BC
mà B,A,C thẳng hàng
nên A nằm giữa B và C
Bài 6:
a: MN+NP=MP
mà M,N,P thẳng hàng
nên N nằm giữa M và P
b: MP+PN=MN
mà M,P,N thẳng hàng
nên P nằm giữa M và N
c: PN+NM=PM
mà P,N,M thẳng hàng
nên N nằm giữa P và M