K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
0
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2022
Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)
HK
1
HN
13 tháng 10 2021
Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).
H
29 tháng 5 2023
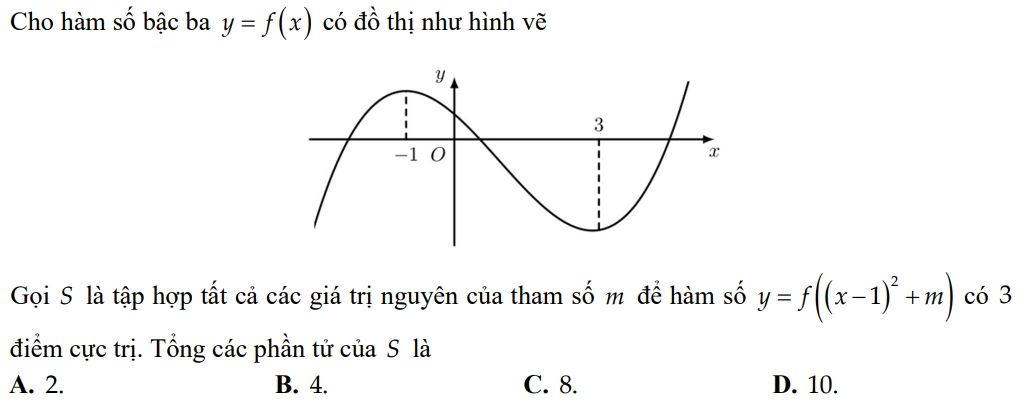
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=1\Rightarrow y=0\\x=-1\Rightarrow y=0\end{matrix}\right.\)
\(\Rightarrow A\left(0;1\right);B\left(1;0\right);C\left(-1;0\right)\)
\(S=\dfrac{1}{2}.\left|y_A-y_B\right|.\left|x_B-x_C\right|=\dfrac{1}{2}.1.2=1\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
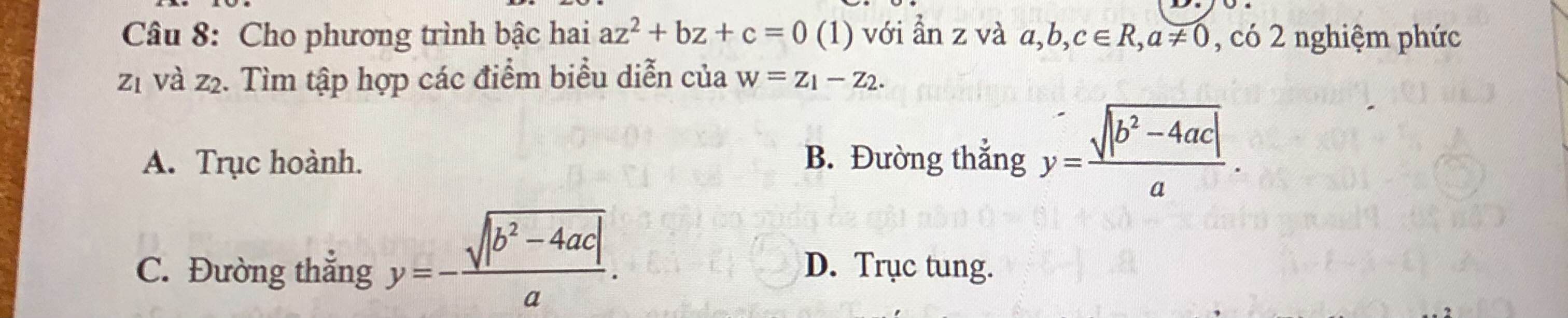
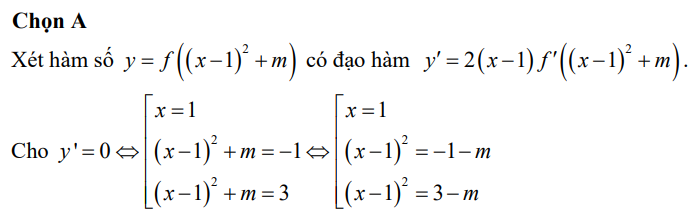
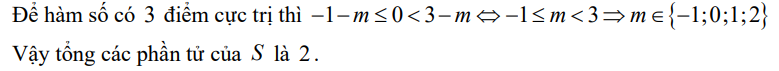
\(lim_{x\rightarrow2}f\left(x\right)=lim_{x\rightarrow2}\frac{\sqrt{x+7}-3}{a\left(x-2\right)}\)
\(=lim_{x\rightarrow2}\frac{x+7-9}{a\left(x-2\right)\left(\sqrt{x+7}+3\right)}=lim_{x\rightarrow2}\frac{1}{a\left(\sqrt{2+7}+3\right)}=\frac{1}{6a}\)
Để hàm số f(x) liên tục trên TXĐ \(lim_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
\(\frac{1}{6a}=3\Leftrightarrow a=\frac{1}{18}\)