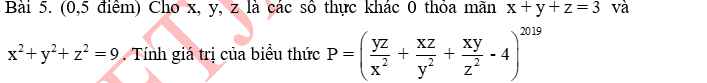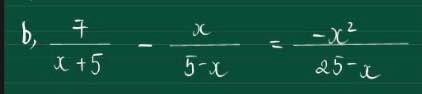Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.Áp dụng định lý pitago vào tam giác vuông PKQ, ta có:
\(QK^2=PQ^2+PK^2\)
\(\Rightarrow QK=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
Áp dụng t/c đường phân giác góc P, ta có:
\(\dfrac{PQ}{PK}=\dfrac{AP}{AK}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{3}{4}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{AK}{4}=\dfrac{AP}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{AK}{4}=\dfrac{AP}{3}=\dfrac{AK+AP}{4+3}=\dfrac{QK}{7}=\dfrac{10}{7}\)
\(\Rightarrow AK=\dfrac{10}{7}.4=\dfrac{40}{7}cm\)
\(\Rightarrow AP=\dfrac{10}{7}.3=\dfrac{30}{7}cm\)
b. Xét tam giác PBQ và tam giác PQK, có:
\(\widehat{PBQ}=\widehat{QPK}=90^0\)
\(\widehat{Q}:chung\)
Vậy tam giác PBQ đồng dạng tam giác PQK ( g.g )
\(\Rightarrow\dfrac{PB}{PK}=\dfrac{PQ}{QK}\)
\(\Leftrightarrow\dfrac{PB}{8}=\dfrac{6}{10}\) \(\Leftrightarrow\dfrac{PB}{8}=\dfrac{3}{5}\)
\(\Leftrightarrow5PB=24\) \(\Leftrightarrow PB=\dfrac{24}{5}cm\)
c. Xét tam giác PBQ và tam giác PBK, có:
\(\widehat{PBQ}=\widehat{PBK}=90^0\)
\(\widehat{PQB}=\widehat{BPK}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác PBQ đồng dạng tam giác PBK ( g.g )
\(\Rightarrow\dfrac{PB}{BK}=\dfrac{QB}{PB}\)
\(\Leftrightarrow PB^2=BK.QB\)

6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

(3-12x)(x-1)+(12x-8)(x+2)+x2=52
3(x-1)-12x(x-1)+12x(x+2)-8(x+2)+x2=52
3x-3-12x2+12+12x2+24x-8x-16+x2=52
(3x+24x-8x)+(12-3-16)+(12x2-12x2+x2)=52
19x-7+x2=52
x(19-x)=52+7=59
mà 59 là số ng tố nên x rỗng
Vậy x E \(\theta\)

xét :
|2x - 1| = 2x - 1 nếu 2x - 1 >0 hay x > \(\frac{1}{2}\)
=> 4(2x - 1) - x = 2 <=> 8x - 4 -x = 2 <=> 7x = 6 => x = \(\frac{6}{7}\)
( thỏa mãn ĐK )
|2x -1| = 1 - 2x nếu 2x - 1 < 0 hay x < \(\frac{1}{2}\)
=> 4.( 1 - 2x) - x = 2 <=> 4 - 8x -x = 2<=> 2 =9x => x = \(\frac{2}{9}\) (thỏa mãn ĐK)
vậy phương trình có nghiệm s = { \(\frac{1}{2},\frac{2}{9}\) }


Sửa đề: \(\dfrac{7}{x+5}-\dfrac{x}{5-x}=\dfrac{-x^2}{25-x^2}\)
\(\Leftrightarrow7\left(x-5\right)+x\left(x+5\right)=x^2\)
\(\Leftrightarrow7x-35+5x=0\)
=>12x=35
hay x=35/12


e: 7x<=9x-5
=>7x-9x<=-5
=>-2x<=-5
=>x>=5/2
f: \(\Leftrightarrow7x-5< 8\left(3x-1\right)-4\left(2x+4\right)\)
=>7x-5<24x-8-8x-16
=>7x-5<16x-24
=>-9x<-19
hay x>19/9

 ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái