Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc lúc về. Điều kiện: x > 0
Ta có vận tốc lúc đi là x + 10 (km/h)
Thời gian lúc đi là 150/(x + 10) (giờ)
Thời gian lúc về là 150/x (giờ)
Thời gian nghỉ là 3 giờ 15 phút = 3.(1/4) (giờ) = 13/4 (giờ)
Theo đề bài, ta có phương trình:
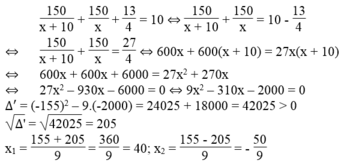
Giá trị x = - 50/9 không thỏa mãn điều kiện bài toán.
Vậy vận tốc ô tô lúc về là 40km/h.

Gọi quãng đường từ Hà Nội - Thanh Hóa là : x
Thời gian đi nửa quãng đường : \(\frac{x}{2.40}\)
Thời gian đi nữa quảng đường còn lại: \(\frac{x}{2.\left(40+20\right)}\)
Thời gian đi về \(:\frac{x}{50}\)
Tổng thời gian đi là: 9h2p - 2h30p = 6h32 p \(=\frac{98}{15}h\)
Ta có phương trình:
\(\frac{a}{2.40}+\frac{a}{2.\left(40+20\right)}+\frac{a}{50}=\frac{98}{15}\)
\(\Leftrightarrow a=160\)
Vậy quãng đường Hà Nội-Thanh Hóa daì 160km

Lời giải:
Thời gian cả đi lẫn về (không tính nghỉ là):
$7h-1h30'=5h30'=5,5h$
Gọi vận tốc lúc đi là $a$ km/h thì vận tốc lúc về là: $a+10$ km/h
Thời gian lẫn về là:
$\frac{150}{a}+\frac{150}{a+10}=5,5$
Giải pt trên với điều kiện $a>0$ ta thu được $a=50$ (km/h)

Lời giải:
Giả sử vận tốc xe máy là $a$ km/h thì vận tốc ô tô là $a+15$ km/h
Xe máy xuất phát trước ô tô 30 phút mà đến sau ô tô 15 phút, tức là thời gian xe máy đi quãng đường HN-TH dài hơn ô tô 45 phút, hay $\frac{3}{4}$ h
Ta có:
Thời gian xe máy đi là: $\frac{135}{a}$ (h)
Thời gian ô tô đi: $\frac{135}{a+15}$ (h)
Theo bài ra: $\frac{135}{a}-\frac{135}{a+15}=\frac{3}{4}$
$\Leftrightarrow a(a+15)=2700$
$\Leftrightarrow (a-45)(a+60)=0$
Vì $a>0$ nên $a=45$ (km/h) -- đây chính là vận tốc xe máy
Vận tốc ô tô là: $45+15=60$ (km/h)

thời gian đi là :
10-(3+15/60)=6.75 h
ta có phương trình là :
150/X+150/(X-10)=6.75
=>X=50 km/h