
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


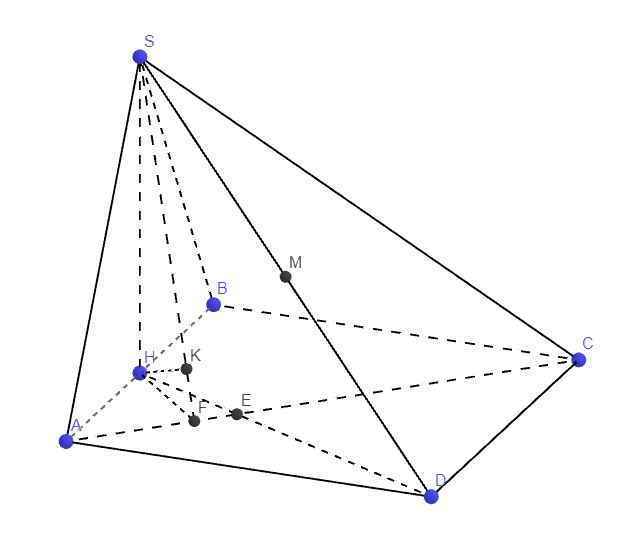
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)

bài này dễ thôi bạn
thay x= x+ k6pi vào hàm số y=f(x)= sin\(\frac{x}{3}\) ta dc
sin\(\frac{x+k6pi}{3}\) =sin\(\frac{x}{3}+k2pi\) ( vì k2pi "số chẵn lần của π" nên có thể bỏ được)
suy ra sin\(\frac{x}{3}\) =sin\(\frac{x}{3}\) =f(x) ( dpcm)

Thiểu năng hết rồi à? Chữ này xấu nhưng không đến mức không đọc được.
P/s: chưa học sin cos nên ko rõ



dùng ông thức hạ bậc
cos2a=\(\dfrac{1+cos2a}{2}\)
pt<=>1+cos(4x+\(\dfrac{2\Pi}{3}\))-3sin(2x+\(\dfrac{5\Pi}{6}\))+1=0
<=>-\(\dfrac{1}{2}\)cos4x-\(\dfrac{\sqrt{3}}{2}\)sin4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x-\(\dfrac{3}{2}\)cos2x+2=0
<=>(-\(\dfrac{1}{2}\)cos4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)+(-\(\sqrt{3}\)sin2x.cos2x-\(\dfrac{3}{2}\)cos2x)=0
<=>[-\(\dfrac{1}{2}\)(1-2sin22x)+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin22x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+\(\dfrac{3}{2}\))-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x+\(\sqrt{3}\))-cos2x.(sin2x+\(\dfrac{\sqrt{3}}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x-cos2x+\(\sqrt{3}\))=0
tới đây bạn tự giải nhé

cau 12:
gọi E là trung điểm AB \(\Rightarrow\)MẸ//BC ; và EN// AC do do ME=BD/2 ;NE= AC/2
\(\Rightarrow\left[\widehat{BD;AC}\right]=\left[\widehat{ME;EN}\right]=90^0\)
\(\Delta MEN\)vuông tại E\(\Rightarrow MN^2=ME^2+NE^2=\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2=\left(\dfrac{10a^2}{4}\right)\Rightarrow MN=\dfrac{a\sqrt{10}}{2}\)
chọn đáp án A
vẽ hình ở ngoài rồi dán vào ko biết tại sao nó lại thụt xuống dưới![]()
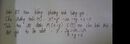


 cho e hỏi sai chỗ nào đc k ạ
cho e hỏi sai chỗ nào đc k ạ

 giúp t với ạ
giúp t với ạ
 giúp mình với ạ
giúp mình với ạ


