KS
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 9 2021
Biết rằng parabol (P): y=ax2+bx-1 qua điểm A(3;-7) và có hoành độ đỉnh bằng 1. Tính giá trị của biểu thức 2a+b . Các bạn ơi đề bài bị sai dề bài này mới chính xác
LT
2
24 tháng 1 2017
http://www.slideshare.net/dotuanhai/de-ts-10-thanh-hoa-tu-nam-2000-den-2014
A
2
DL
10 tháng 10 2021
Tìm 2 số , biết rằng tổng gấp 7 lần hiệu của chúng,còn tích của chúng gấp 192 lần hiệu của chúng
LM
5
31 tháng 10 2021
Giải và biện luận phương trình sau theo tham số m: m(x – 4) = 5x – 2.
\(m\left(x-4\right)=5x-2\\ \Rightarrow mx-4x=5x-2\\\Rightarrow mx-5x=4x-2\\ \Rightarrow x\left(m-5\right)=4x-2 \)
Trong trường hợp phương trình có nghiệm duy nhất thì
\(m-5\ne0\\ \Rightarrow m\ne5\)=> \(x=\frac{4m-2}{m-5}\)
Còn trong trường hợp m - 5 = 0 <=> m = 5 thì
\(x=\frac{20-2}{5-5}=>0.x=18\)
=> Phương trình vô nghiệm
Vậy ta có kết luận
Phương trình có nghiệm duy nhất khi \(m\ne5\)
Phương trình vô nghiệm khi m = 5
LM
3
29 tháng 10 2021
m(x – 4) = 5x – 2 ⇔(m - 5)x = 4m - 2
Nếu m - 5 ≠ 0 ⇔ m ≠ 5 thì phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Nếu m – 5 = 0 ⇔ m = 5, phương trình trở thành:
0.x = 18 ⇒ phương trình vô nghiệm
Vậy với m ≠ 5 phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Với m = 5 phương trình vô nghiệm.
14 tháng 12 2021
m(x – 4) = 5x – 2 ⇔(m - 5)x = 4m - 2
Nếu m - 5 ≠ 0 ⇔ m ≠ 5 thì phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Nếu m – 5 = 0 ⇔ m = 5, phương trình trở thành:
0.x = 18 ⇒ phương trình vô nghiệm
Vậy với m ≠ 5 phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Với m = 5 phương trình vô nghiệm.
30 tháng 10 2021
Kêu nếu chép mạng thì cho thêm báo cáo vs báo admin mà vẫn chép kìa . 2k9 làm lớp 10 .Giỏi đấy :))
Làm thử , ko vừa ý thì bỏ qua nha .
Bài làm :
\(m\left(x-1\right)=5x-2\)
\(\Leftrightarrow mx-4m-5x=-2\)
\(\Leftrightarrow\left(m-5\right)x=4m-2\left(1\right)\)
+) Với m - 5 # 0
=> ( 1 ) có nghiệm \(x=\frac{4m-2}{m-5}\)
+) Với \(\hept{\begin{cases}m-5=0\\4m-2\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\m\ne\frac{1}{2}\end{cases}}}\)
=> ( 1 ) trở thành 0x = 18
=> Pt vô nghiệm
+) với \(\hept{\begin{cases}m-5=0\\4m-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}m=5\\m=\frac{1}{2}\end{cases}}}\)
=> ( 1 ) trở thành 0x = 0
=> Pt có vô số nghiệm
KA
30 tháng 10 2021
m(x – 4) = 5x – 2 ⇔(m - 5)x = 4m - 2
Nếu m - 5 ≠ 0 ⇔ m ≠ 5 thì phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Nếu m – 5 = 0 ⇔ m = 5, phương trình trở thành:
0.x = 18 ⇒ phương trình vô nghiệm
Vậy với m ≠ 5 phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Với m = 5 phương trình vô nghiệm.
11 tháng 8 2021
Phương trình đường tròn ngoại tiếp tam giác 
ABC có tâm K(
;3). và bán kính R =AK=
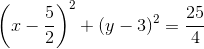
Phân giác AI có phương trình 
3x+y-8=0
Gọi D=AI 
(K)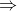 
tọa độ điểm D là nghiệm của hệ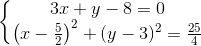 
Giải rât được hai nghiệm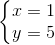 
và 
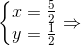D()
Lại có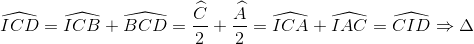 
ICD cân tại D
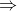DC=DI mà DC=DB 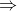B, C là nghiệm của hệ:
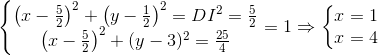
Vậy B, C có tọa độ là (1;1), (4;1)
24 tháng 7 2021
Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.