
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,\Leftrightarrow\left(x-5\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-4\right)\left(3x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{3}\end{matrix}\right.\\ c,\Leftrightarrow\left(x-7\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ d,\Leftrightarrow\left(2x+3\right)\left(2x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\\ 2,\\ a,\Leftrightarrow\left(x+5\right)^2=0\Leftrightarrow x=-5\\ b,\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x=\dfrac{1}{2}\\ c,\Leftrightarrow\left(x-9\right)^2=0\Leftrightarrow x=9\\ d,\Leftrightarrow\left(x-3\right)^3=0\Leftrightarrow x=3\\ e,\Leftrightarrow3x\left(x^2-2x+3\right)=0\\ \Leftrightarrow3x\left(x^2-2x+1+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x-1\right)^2+2=0\left(vô.nghiệm\right)\end{matrix}\right.\\ \Leftrightarrow x=0\)
\(f,\Leftrightarrow3x\left(x^2-4x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Bài 1:
a) \(\Rightarrow\left(x-5\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)
b) \(\Rightarrow3x\left(x-4\right)-\left(x-4\right)=0\)
\(\Rightarrow\left(x-4\right)\left(3x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{3}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-7\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow\left(x+5\right)^2=0\Rightarrow x=-5\)
b) \(\Rightarrow\left(x-\dfrac{1}{2}\right)^2=0\Rightarrow x=\dfrac{1}{2}\)
c) \(\Rightarrow\left(x-9\right)^2=0\Rightarrow x=9\)
d) \(\Rightarrow\left(x-3\right)^3=0\Rightarrow x=3\)
e) \(\Rightarrow3x\left(x^2-6x+9\right)=0\)
\(\Rightarrow3x\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
f) \(\Rightarrow3x\left(x^2-4x+4\right)=0\)
\(\Rightarrow3x\left(x-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

<=> 7x-1>0 và 3-2x<0 hoặc 7x-1<0 và 3-2x>0
<=> x>1/7 và x>3/2 hoặc x<1/7 và x<3/2
<=> x>3/2 hoặc x<1/7
Vậy với x>3/2 hoặc x<1/7 thì thỏa mãn đề bài
(những chữ "hoặc" và chữ "và" bạn có thể thay bằng dấu ngoặc vuông và ngoặc nhọn nhé!!!)
Have a good day!!!

tất cả các ý mình cm thành cụm luôn nhé
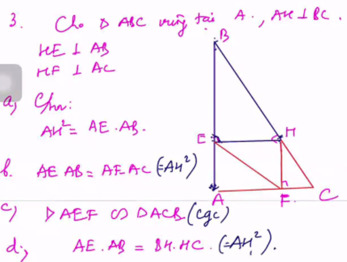
Xét tam giác AHE và tam giác ABH ta có
^A _ chung
^AHE = ABH = 900
Vậy tam giác AHE ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AE}{AH}\Rightarrow AH^2=AE.AB\)(1)
Xét tam giác AHC và tam giác AFH có
^A _ chung
^AHC = ^AFH = 900
Vậy tam giác AHC ~ tam giác AFH (g.g)
\(\dfrac{AH}{AF}=\dfrac{AC}{AH}\Rightarrow AH^2=AF.AC\)(2)
Từ (1) ; (2) suy ra \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(*)
Xét tam giác AEF và tam giác ABC có
^A _ chung ; có (*)
Vậy tam giác AEF ~ tam giác ABC (c.g.c)

Bài 15:
\(P=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{x-y}{2xy}\cdot\dfrac{xy+y^2+xy-y^2}{x\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{x}\)

\(\dfrac{x+1}{2x^2-x^4}=\dfrac{x+1}{x^2\left(2-x^2\right)}=\dfrac{-\left(x+1\right)\left(x^4+2x^2+4\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{x}{x^4+2x^2+4}=\dfrac{x^3\left(x^2-2\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{2x-1}{x^7-8x}=\dfrac{2x-1}{x\left(x^6-8\right)}=\dfrac{x\left(2x-1\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\)

Chỉ khi x + y + z = 0 mới như vậy.
Cụ thể :
Ta có :
\(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy^2-3x^2y-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2+z^2-\left(x+y\right)z\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left[x^2+y^2+2xy+z^2-xz-yz-3xy\right]\)
\(=0\) là BS xyz

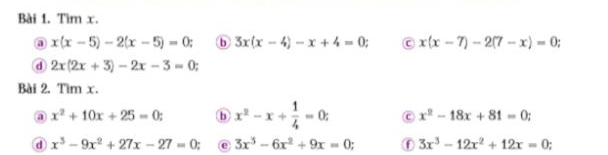

 cd
cd