
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{110}\)
= \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{10.11}\)
= \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
= \(1-\dfrac{1}{11}\)
= \(\dfrac{10}{11}\)
Vậy A = \(\dfrac{10}{11}\)
a) \(A=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{110}\)
\(\Leftrightarrow A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{10.11}\)
\(\Leftrightarrow A=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(\Leftrightarrow A=1-\dfrac{1}{11}=\dfrac{10}{11}\)

\(a.\dfrac{3}{5}-\dfrac{-7}{10}-\dfrac{13}{-20}=\dfrac{12}{20}-\dfrac{-14}{20}-\dfrac{-13}{20}=\dfrac{12-\left(-14\right)-\left(-13\right)}{20}=\dfrac{39}{20}\)
\(b.\dfrac{3}{4}+\dfrac{-1}{3}-\dfrac{5}{18}=\dfrac{3}{4}+\left(\dfrac{-6}{18}-\dfrac{5}{18}\right)=\dfrac{3}{4}+\dfrac{-11}{18}=\dfrac{27}{36}-\dfrac{-22}{36}=\dfrac{49}{36}\)
\(c.\dfrac{3}{13}-\dfrac{5}{-8}+\dfrac{-1}{2}=\dfrac{3}{13}-\left(\dfrac{5}{-8}+\dfrac{-4}{8}\right)=\dfrac{3}{13}-\dfrac{1}{8}=\dfrac{24}{104}-\dfrac{13}{104}=\dfrac{11}{104}\)
\(d.\dfrac{1}{2}+\dfrac{1}{-3}=\dfrac{3}{6}+\dfrac{-2}{6}=\dfrac{1}{6}\)
\(a,\dfrac{3}{5}-\dfrac{-7}{10}-\dfrac{13}{-20}\)
\(=\dfrac{12}{20}+\dfrac{14}{20}+\dfrac{13}{20}\)
\(=\dfrac{12+14+13}{20}\)
\(=\dfrac{39}{20}\)
\(b,\dfrac{3}{4}+\dfrac{-1}{3}-\dfrac{5}{18}\)
\(=\dfrac{27}{36}+\dfrac{-12}{36}-\dfrac{10}{36}\)
\(=\dfrac{27+\left(-12\right)-10}{36}\)
\(=\dfrac{5}{36}\)
\(c,\dfrac{3}{13}-\dfrac{5}{-8}+\dfrac{-1}{2}\)
\(=\dfrac{24}{104}-\dfrac{-65}{104}+\dfrac{-52}{104}\)
\(=\dfrac{24-\left(-65\right)+\left(-52\right)}{104}\)
\(=\dfrac{37}{104}\)
\(d,\dfrac{1}{2}+\dfrac{1}{-3}\)
\(=\dfrac{3}{6}+\dfrac{-2}{6}\)
\(=\dfrac{3+\left(-2\right)}{6}\)
\(=\dfrac{1}{6}\)

Nếu:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+n}{b+n}< 1\left(n\in N\right)\)
\(B=\dfrac{10^{20}+1}{10^{21}+1}< 1\)
\(B< \dfrac{10^{20}+1+9}{10^{21}+1+9}\Rightarrow B< \dfrac{10^{20}+10}{10^{21}+10}\Rightarrow B< \dfrac{10\left(10^{19}+1\right)}{10\left(10^{20}+1\right)}\Rightarrow B< \dfrac{10^{19}+1}{10^{20}+1}=A\)\(\Rightarrow B< A\)

\(\Leftrightarrow5\cdot\dfrac{5-4-2}{20}< \dfrac{x}{20}< =3\cdot\dfrac{10-5-4}{20}\)
=>-1/20<x/20<=3/20
=>-1<x<=3
hay \(x\in\left\{0;1;2;3\right\}\)

a) (1/7.x-2/7).(-1/5.x-2/5)=0
=> 1/7.x-2/7=0hoặc-1/5.x-2/5=0
*1/7.x-2/7=0
1/7.x=0+2/7
1/7.x=2/7
x=2/7:1/7
x=2
b)1/6.x+1/10.x-4/5.x+1=0
(1/6+1/10-4/5).x+1=0
(1/6+1/10-4/5).x=0-1
(1/6+1/10-4/5).x=-1
(-8/15).x=-1
x=-1:(-8/15) =15/8

2) Tinh nhanh:
a) \(\dfrac{5}{23}\) . \(\dfrac{17}{26}\) + \(\dfrac{5}{23}\) . \(\dfrac{10}{26}\) - \(\dfrac{5}{23}\)
= \(\dfrac{5}{23}\) . \(\left(\dfrac{17}{26}+\dfrac{10}{26}-1\right)\)
= \(\dfrac{5}{23}\) . \(\left(\dfrac{27}{26}-1\right)\) = \(\dfrac{5}{23}\) . \(\dfrac{1}{26}\)
= \(\dfrac{5}{598}\)
b) \(\dfrac{1}{7}.\dfrac{5}{9}+\dfrac{5}{9}.\dfrac{2}{7}+\dfrac{5}{9}.\dfrac{1}{7}+\dfrac{5}{9}.\dfrac{3}{7}\)
= \(\dfrac{5}{9}.\left(\dfrac{1}{7}+\dfrac{2}{7}+\dfrac{1}{7}+\dfrac{3}{7}\right)\)
= \(\dfrac{5}{9}\) . 1= \(\dfrac{5}{9}\)
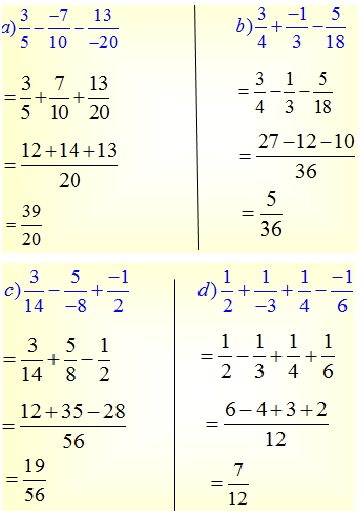
\(A=\dfrac{1}{2^0.5}+\dfrac{1}{2^1.5}+\dfrac{1}{2^2.5}+...+\dfrac{1}{2^8.5}\)
\(5A=\dfrac{1}{2^0}+\dfrac{1}{2^1}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^8}\)
\(5A=2-1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+...++\dfrac{1}{128}+\dfrac{1}{256}\)
\(5A=2-\dfrac{1}{256}=\dfrac{511}{256}\)
\(A=\dfrac{511}{1280}\)
1/5 + 1/5 - 1/10 + 1/10 - 1/20 + 1/20 - 1/40 + ... + 1/640 - 1/1280
= 1/5 + 1/5 - 1/1280 = 511/1280