Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
$\frac{2}{3}x-\frac{7}{6}=\frac{12}{7}-\frac{1}{2}=\frac{17}{14}$
$\frac{2}{3}x=\frac{17}{14}+\frac{7}{6}=\frac{50}{21}$
$x=\frac{50}{21}: \frac{2}{3}=\frac{25}{7}$
b.
$(1\frac{1}{2}+\frac{5}{3}-\frac{1}{6}):x=\frac{3}{4}-\frac{1}{2}$
$3:x=\frac{1}{4}$
$x=3: \frac{1}{4}=12$

\(a.x+\dfrac{1}{6}=-\dfrac{3}{8}\)
\(\Leftrightarrow x=-\dfrac{13}{24}\)
\(b.2-\left(\dfrac{3}{4}-x\right)=\dfrac{7}{12}\)
\(\Leftrightarrow2-\dfrac{3}{4}+x=\dfrac{7}{12}\)
\(\Leftrightarrow x=-\dfrac{2}{3}\)
\(c.\dfrac{1}{2}x+\dfrac{1}{8}x=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{5}{8}x=\dfrac{3}{4}\)
\(\Leftrightarrow x=\dfrac{6}{5}\)
\(d.75\%-1\dfrac{1}{2}+0,5:\dfrac{5}{12}-\left(\dfrac{-1}{2}\right)^2\)
\(=\dfrac{75}{100}-\dfrac{3}{2}+\dfrac{1}{2}:\dfrac{5}{12}-\dfrac{1}{4}\)
\(=-\dfrac{3}{4}+\dfrac{6}{5}-\dfrac{1}{4}\)
\(=\dfrac{1}{5}\)
a) \(x+\dfrac{1}{6}=\dfrac{-3}{8}\)
\(x=\dfrac{-3}{8}-\dfrac{1}{6}\)
\(x=\dfrac{-13}{24}\)
vậy x =....
b) \(2-\left(\dfrac{3}{4}-x\right)=\dfrac{7}{12}\)
\(\dfrac{3}{4}-x=2-\dfrac{7}{12}\)
\(\dfrac{3}{4}-x=\dfrac{17}{12}\)
\(x=\dfrac{3}{4}-\dfrac{17}{12}\)
\(x=\dfrac{-2}{3}\)
vậy x =....

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 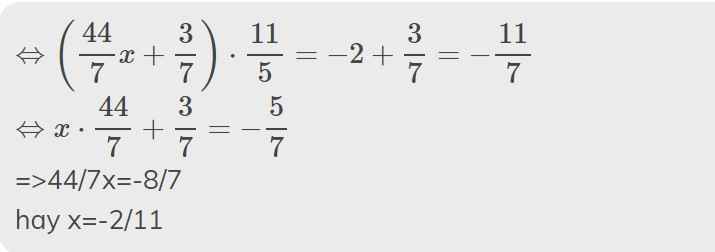
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

\(\dfrac{x}{5}+\dfrac{1}{2}=\dfrac{6}{10}\Leftrightarrow\dfrac{x}{5}=\dfrac{6}{10}-\dfrac{1}{2}\Rightarrow x=\dfrac{1}{10}\)

a: =>3/2x=64/15
=>x=128/45
b: =>-1/6x=7/12
=>x=-7/2
c: =>11/2*x=1/2
=>x=1/2:11/2=1/11

a: =>6/x=x/24
=>x^2=144
=>x=12 hoặc x=-12
b: =>x(1-7/12+3/8)=5/24
=>x*19/24=5/24
=>x=5/24:19/24=5/19
c: =>(x-1/3)^2=1+3/4+1/2=9/4
=>x-1/3=3/2 hoặc x-1/3=-3/2
=>x=11/6 hoặc x=-7/6
d: =>(x-3)^2=16
=>x-3=4 hoặc x-3=-4
=>x=-1 hoặc x=7
e: =>9/x=-1/3
=>x=-27
f: =>x-1/2=0 hoặc -x/2-3=0
=>x=1/2 hoặc x=-6

a, \(x\) : \(\dfrac{13}{3}\) = -2,5
\(x\) = -2,5 . \(\dfrac{13}{3}\)
\(x\) = \(\dfrac{65}{6}\)
b,\(\dfrac{3}{5}\)\(x\) = \(\dfrac{1}{10}-\)\(\dfrac{1}{4}\)
\(\dfrac{3}{5}x\) = \(\dfrac{-3}{20}\)
\(x\) = \(\dfrac{-3}{20}\) : \(\dfrac{3}{5}\)
\(x\) = \(\dfrac{-1}{4}\)
c, \(\dfrac{25}{9}-\dfrac{12}{13}x=\dfrac{7}{9}\)
\(\dfrac{12}{13}x\)\(=\dfrac{25}{9}-\dfrac{7}{9}\)
\(\dfrac{12}{13}x=2\)
\(x=2:\dfrac{12}{13}\)
\(x=\dfrac{13}{6}\)

a) (2x - 3)(6 - 2x) = 0
=> \(\left[{}\begin{matrix}2x-3=0\\6-2x=0\end{matrix}\right.=>\left[{}\begin{matrix}2x=3\\2x=6\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\end{matrix}\right.\)
b) \(5\dfrac{4}{7}:x=13=>\dfrac{39}{7}:x=13=>x=\dfrac{39}{7}:13=>x=\dfrac{3}{7}\)
c) \(2x-\dfrac{3}{7}=6\dfrac{2}{7}=>2x-\dfrac{3}{7}=\dfrac{44}{7}=>2x=\dfrac{47}{7}=>x=\dfrac{47}{14}\)
d) \(\dfrac{x}{5}+\dfrac{1}{2}=\dfrac{6}{10}=>\dfrac{x}{5}=\dfrac{6}{10}-\dfrac{1}{2}=>\dfrac{x}{5}=\dfrac{1}{10}=>x.10=5=>x=\dfrac{1}{2}\)
e) \(\dfrac{x+3}{15}=\dfrac{1}{3}=>\left(x+3\right).3=15=>x+3=5=>x=2\)

\(\dfrac{1}{5}+\dfrac{2}{11}< \dfrac{x}{55}< \dfrac{2}{5}+\dfrac{1}{5}\)
\(\dfrac{11+10}{55}< \dfrac{x}{55}< \dfrac{3}{5}\)
\(\dfrac{21}{55}< \dfrac{x}{55}< \dfrac{33}{55}\)
Vậy \(x\in\left\{22;23;24;...\right\}\)
x có nghĩa là nhân nha
Câu đầu sai đề nhé! Phải là 2007 chứ ko phải 20007!
\(A=\dfrac{1}{2}\cdot\dfrac{1}{7}+\dfrac{1}{7}\cdot\dfrac{1}{12}+...+\dfrac{1}{2002}\cdot\dfrac{1}{2007}\\ =\dfrac{1}{2\cdot7}+\dfrac{1}{7\cdot12}+...+\dfrac{1}{2002\cdot2007}\\ =\dfrac{1}{5}\left(\dfrac{5}{2\cdot7}+\dfrac{5}{7\cdot12}+...+\dfrac{5}{2002+2007}\right)\\ =\dfrac{1}{5}\cdot\left(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+...+\dfrac{1}{2002}-\dfrac{1}{2007}\right)\\ =\dfrac{1}{5}\left(\dfrac{1}{2}-\dfrac{1}{2007}\right)\\ =\dfrac{1}{5}\cdot\dfrac{2005}{4014}\\ =\dfrac{401}{4014}\)
\(B=\left(1+\dfrac{1}{2}\right)\cdot\left(1+\dfrac{1}{3}\right)...\left(1+\dfrac{1}{2007}\right)\\B=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot\cdot\cdot\dfrac{2008}{2007}\\ B=\dfrac{3\cdot4\cdot...\cdot2008}{2\cdot3\cdot...\cdot2007}\\ B=\dfrac{2008}{2}\\ B=1004 \)
\(C=\left(1-\dfrac{1}{2}\right)\cdot\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2008}\right)\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2007}{2008}\\ =\dfrac{1\cdot2\cdot...\cdot2007}{2\cdot3\cdot...\cdot2008}\\ =\dfrac{1}{2008}\)