Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Vì ∆ABC cân tại A
Mà AM là trung tuyến BC
=> AM là trung trực và phân giác ∆ABC
=> BAM = CAM
Gọi O là giao điểm AM và DE
Mà OAC = OAD ( đối đỉnh )
BAO = OAE ( đối đỉnh )
Mà BAO = CAO (cmt)
=> OAD = OAE
Hay AO là phân giác DAE(1)
Mà AD = AE
=> ∆ADE cân tại A(2)
Từ (1) và (2)
=> AO là trung trực ∆ADE
=> AO = OC
AO\(\perp\)DE
Hay D và E đối xứng qua AM

A B C D E M I
Bài làm
Gọi giao điểm của MA và ED là I
Xét tam giác cân ABC có:
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
\(\Rightarrow\widehat{B}=\frac{180^0-\widehat{EAD}}{2}\) ( 1 )
Xét tam giác cân AED có: ( Vì EA = DA )
=> \(\widehat{E}=\widehat{D}\)
\(\Rightarrow\widehat{D}=\frac{180^0-\widehat{BAC}}{2}\)( 2 )
Mà \(\widehat{BAC}=\widehat{EAD}\)( Hai góc đối đỉnh )
Từ ( 1 ) và ( 2 ) => \(\widehat{B}=\widehat{D}\)
Mà hai góc này ở vị trí so le trong
=> ED // AM ( 3 )
Ta có: Tam giác ABC là tam giác cân.
Và M là trung điểm của BC
=> AM là đường trung tuyến của tam giác ABC
=> AM cũng là đường cao
=> AM | BC ( 4 )
Từ ( 3 ) và ( 4 ) => AI | ED
=> AI cũng là đường cao của ED
Và tam giác AED là tam giác cân
=> MA cũng là đường trung tuyến của của ED
=> EI = ID
=> E đối xứng với cả D qua AI
hay E đối xứng với D qua AM ( đpcm )
# Học tốt #

a)Xét tứ giác ABDC :
AM = MD ; BM = MC
=>Tứ giác ABDC là hình bình hành
Mà góc BAC = 90 = >Tứ giác ABDC là hcn
b)Xét tam giác AID :
AH= HI ; AM = MD (gt)
=> HM song song ID ( đường tb)
=>tứ giác BIDC la ht
AC la trung truc AI = > tam giac ABI can tai B
=> AB = BI ma AB = DC ( ABDC la hcn )=> BI = DC
hay BIDC la hinh thang can
c) Ta có góc ACB = góc AHM = góc AEF
góc BAM = góc ABM
mà góc ABM + góc ACM = 90 => góc AEF + góc BAM = 90 độ hay AM vuông góc EF ( đccm)

1/. Xét Tứ giác AEHF, có:
E = 90 (EH vuong góc AB)
F = 90 (HF vuong AC)
A = 90 (ABC vuong tai A)
=> AEHF là hcn
2/. Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM =1/2BC => AM =MB = MC = 2,5 cm
=> BC = 2,5 x2 = 5cm
Áp dụng định lý Py-ta-go vào tam giác vuông ABC, có:
AB^2 +AC^2 =BC^2
9+AC^2 = 25
=> AC^2 = 25-9 = 16
=> AC =4cm
Diện tích tam giác ABC: 1/2AB.AC = 1/2(.3.4 )= 6cm^2
3/. Gọi K là giao điểm của EF và AM, J là giao điểm của EF và AH
CM: góc AEK = góc ABC
Vì J là giao điểm của 2 đường chéo trong hcn AEHF => ẠJ = JH = Ẹ = JF
=> tam giác EJA cân tại J => AEJ = EAH (1)
Xét tam giác vuông ABH => EAH +ABC = 90
Xét tam giác vuông ABC=> ABC + ACB = 90
=> EAH = ACB và (1) => ACB = AEJ (2)
Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM = BM = MC
=> tam giác ABM cân tại M => EAK = ABC (3)
Xét tam giác EAK: có: AEJ + EAK = ACB + ABC = 90 ( do 2 và 3)
=> tam giác AEK vuong tại K
Hay AM vuông EF
4/. Vì A đới xứng với I qua BC => AI vuông góc với BC . Mà AH vuong với BC => A. H , I thẳng hàng . hay H là trung điểm của AI
Xét tam giác AID, có:
H là trung ddierm của AI, M là trung điểm của AD
=> HM là đường trung bình của tam giác AID => HM // ID
=> tứ giác BIDC là hình thang
Xét tam giác ABI , có: BH vừa là đường cao vừa là đường trung tuyến => ABI cân tại B => IBH = ABH (BH là đường phân giác) (4)
Xét tứ giác ABCD có:
M là trung điểm BC
M là trung điểm AD
M = BC giao AD
=> ABCD là hình bình hành và A = 90 => ABCD là hình chữ nhật
=> DCB = ABC (DC // AB và solle trong) (5)
Từ 4 và 5 => BCD = IBC (= ABC) => Hình thang BIDC là hình thang cân
1/. Xét Tứ giác AEHF, có:
E = 90 (EH vuong góc AB)
F = 90 (HF vuong AC)
A = 90 (ABC vuong tai A)
=> AEHF là hcn
2/. Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM =1/2BC => AM =MB = MC = 2,5 cm
=> BC = 2,5 x2 = 5cm
Áp dụng định lý Py-ta-go vào tam giác vuông ABC, có:
AB^2 +AC^2 =BC^2
9+AC^2 = 25
=> AC^2 = 25-9 = 16
=> AC =4cm
Diện tích tam giác ABC: 1/2AB.AC = 1/2(.3.4 )= 6cm^2
3/.

1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
2: AM=2,5cm nên BC=5cm
=>AC=4cm
S=3x4/2=6cm2
3:
Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AFE=góc AHE=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc ACB
=>góc MAC+góc EFA=90 độ
=>AM vuông góc với EF
4:
Xét ΔADI có
H,M lần lượt là trung điểm của AI và AD
nên HM là đường trung bình
=>HM//DI
=>DI//BC
Xét ΔCIA có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCIA cân tại C
=>CI=CA=DB
=>BIDC là hình thang cân

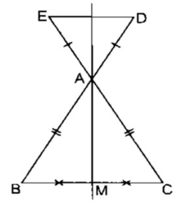
ΔABC cân tại A có AM là đường trung tuyến
⇒ AM là tia phân giác của góc (BAC)
⇒ ∠ (BAM) = ∠ (MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠ (BAM) = ∠ (DAN) (đối đỉnh) (2)
∠ (MAC) = ∠ (NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠ (DAN) = ∠ (NAE)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.

TL :
ht