
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bước 1. Vẽ góc xOy có số đo bằng \(68^0\)
Bước 2. Sử dụng thước đo độ, đánh dấu điểm ứng với vạch \(34^0\) của thước đo góc.
Bước 3. Kẻ tia Oz đi qua điểm đã đánh dấu. Tia Oz là tia phân giác của góc xOy.

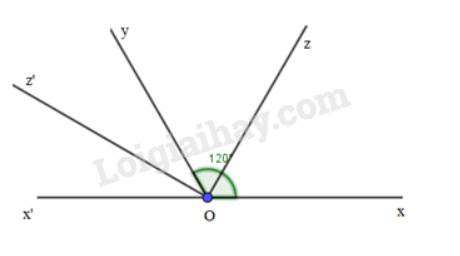
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ = 71^\circ \)
Mà \(\widehat {x'Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên \(\widehat {xOz} + \widehat {x'Oz} = 180^\circ \Rightarrow 71^\circ + \widehat {x'Oz} = 180^\circ \Rightarrow \widehat {x'Oz} = 180^\circ - 71^\circ = 109^\circ \)
Vậy \(\widehat {x'Oz} = 109^\circ \)

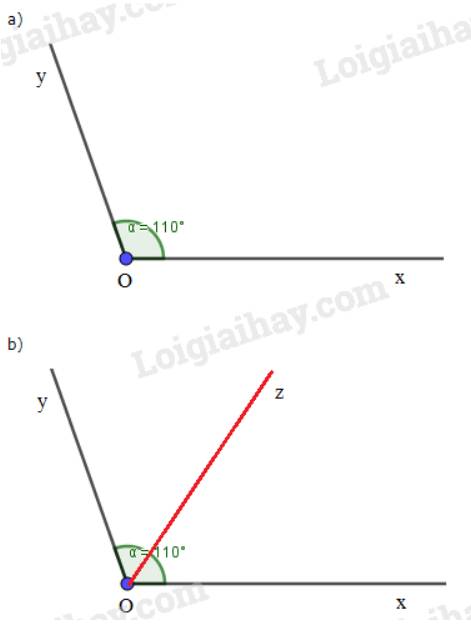
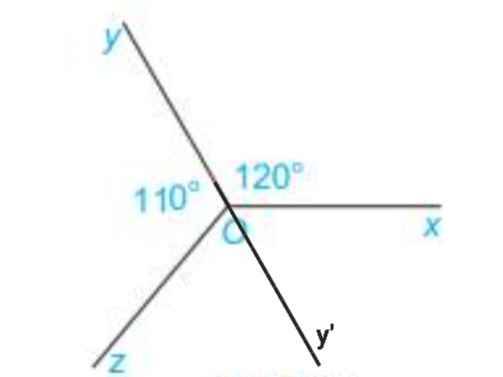 Vẽ tia Oy' là tia đối của tia Oy
Vẽ tia Oy' là tia đối của tia Oy
Ta có:
∠xOy + ∠xOy' = 180⁰ (kề bù)
⇒ ∠xOy' = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰
Lại có:
∠zOy + ∠zOy' = 180⁰ (kề bù)
⇒ ∠zOy' = 180⁰ - ∠zOy
= 180⁰ - 110⁰
= 70⁰
⇒ ∠zOx = ∠zOy' + ∠xOy'
= 70⁰ + 60⁰
= 130⁰
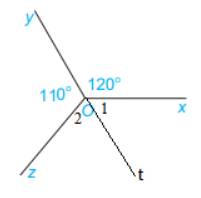
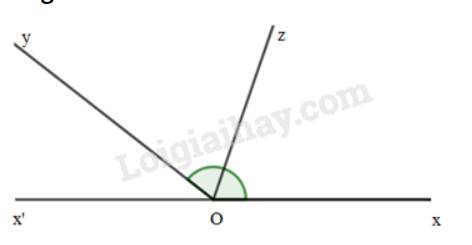
Kẻ Ot là tia đối của tia Oy.
Ta được:+) \(\widehat {{O_1}} + \widehat {xOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{O_1}} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {{O_1}} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
+) \(\widehat {{O_2}} + \widehat {yOz} = 180^\circ \)( 2 góc kề bù)
Vì Ot nằm giữa 2 tia Ox và Oz nên \(\widehat {xOz} = \widehat {{O_1}} + \widehat {{O_2}} = 60^\circ + 70^\circ = 130^\circ \)
Vậy \(\widehat {zOx} = 130^\circ \)

Vẽ góc \(\widehat {xOy} = 120^\circ \)
a) Sử dụng thước thẳng và compa
Bước 1: Trên tia Ox, lấy điểm A bất kì ( A khác O); vẽ một phần đường tròn tâm O, bán kính OA, cắt tia Oy tại điểm B.
Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.
Bước 3: Vẽ một phần đường tròn tâm B bán kính BO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.
Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.
b) Sử dụng thước hai lề
Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Ox, dùng bút vạch một vạch thẳng theo cạnh của thước.
Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Oy, dùng bút vạch một vạch thẳng theo cạnh của thước.
Bước 3: Hai nét vạch thẳng vẽ ở bước 1 và bước 2 cắt nhau tại điểm C nằm trong góc xOy.
Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.

x O y y' x' t t'
+) Tính \(\widehat{yOx'}\)
Ta có: \(\widehat{yOx'}+\widehat{xOy}=180^0\)(kề bù)
hay \(\widehat{yOx'}+36^0=180^0\)
\(\Leftrightarrow\widehat{yOx'}=180^0-36^0\)
\(\Leftrightarrow\widehat{yOx'}=144^0\)
Vậy \(\widehat{yOx'}=144^0\)
+) Tính \(\widehat{y'Ox'}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox'}\) và \(\widehat{yOx}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{y'Ox'}=\widehat{xOy}=36^0\)
Vậy \(\widehat{y'Ox'}=36^0\)
+) Tính \(\widehat{y'Ox}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox}\) và \(\widehat{yOx'}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{yOx'}=\widehat{xOy}'=144^0\)
Vậy \(\widehat{y'Ox}=144^0\)
b) Vì \(\widehat{y'Ox'}=\widehat{xOy}\)mà Ot là tia phân giác của \(\widehat{xOy}\),mà Ot' là tia phân giác của \(\widehat{x'Oy'}\)nên Ot và Ot' (điều hiển nhiên)

a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
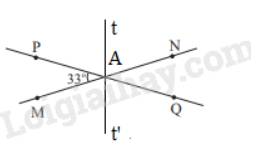
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau


a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy
b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)