Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trường hợp bằng nhau \(g-g-g\) của 1 t/g không tồn tại vì nếu trong 2 tam giác, độ dài của các cạnh có thể thay đổi, không giống với độ dài của tam giác kia nên không xảy ra t/h đó mà có \(c-g-c;g-c-g;c-c-c\)
b) Một tam giác không thể có 2 góc vuông, vì nếu có 2 góc vuông thì nó sẽ trờ thành hình vuông chứ không phải hình tam giác, thế nên tam giác chỉ được có 1 góc vuông.
Cách diễn đạt không được hay cho lắm nên làm ơn thông cảm.
a) Trường hợp góc-góc-góc không tồn tại vì 2 tam giác có số đo từng góc bằng nhau thì chưa chắc các cạnh đã bằng nhau (ví dụ hình dưới)
A B C A` B` C` A = A` B = B` C = C` ^ ^ ^ ^ ^ ^ AB ≠ A`B` BC ≠ B`C` CA ≠ C`A` Như bạn đã thấy, hai tam giác dưới đây không Bằng nhau
b) Ta biết, tổng của một tam giác là 180o, nếu có 2 cạnh trong một tam giác bằng 90o (góc vuông) thì không thể (vì 90o+90o=180o)

Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)

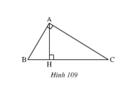
Hai tam giác AHC và BAC có:
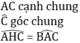
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC
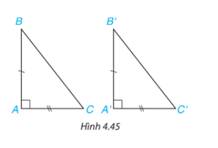
a, Trường hợp góc-góc-góc không tồn tại vì 2 tam giác có số đo từng góc bằng nhau thì chưa chắc các cạnh đã bằng nhau
b, Một tam giác không thể có 2 góc vuông vì tổng 2 góc vuông bằng 1800 mà trong tam giác không có góc nào có số đo bằng 00
Hoặc có thể giải thích :
Vì nếu 2 cạnh của 1 tam giác mà cùng vuông góc với cạnh còn lại thì hai cạnh đó song song với nhau (không cắt nhau). Mà nếu trong 1 hình mà có 2 cạnh song song với nhau thì đó không thể là hình tam giác .
đồng dạng thì sao?