Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1:
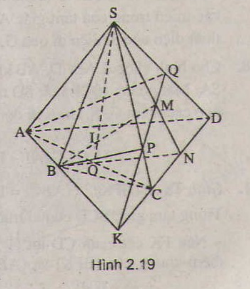
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
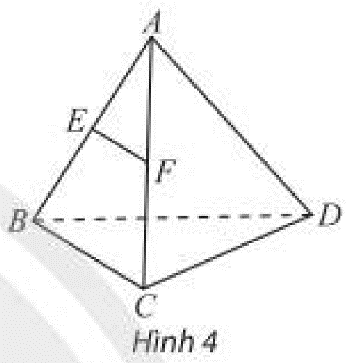
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
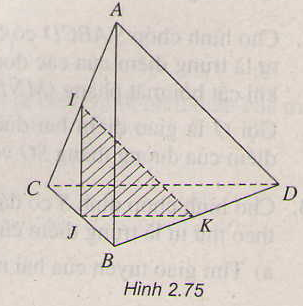
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
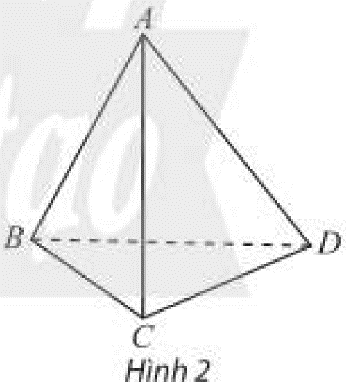
Câu 4:
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
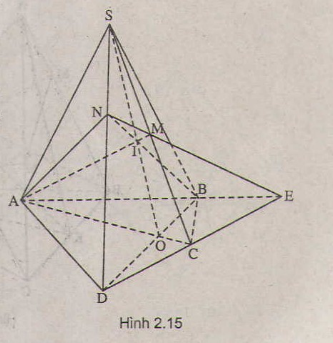
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy
a) Các vị trí tương đối của hai đường thẳng trong mặt phẳng:
- Hai đường thẳng không có điểm chung thì hai đường thẳng song song
- Hai đường thẳng có một điểm chung thì hai đường thẳng cắt nhau
- Hai đường thẳng có rất nhiều điểm chung thì hai đường thẳng trùng nhau
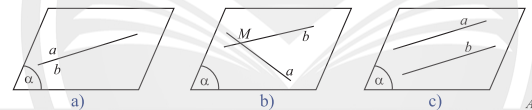
b) Hai đường thẳng a và b ở Hình 31a cùng nằm trong một mặt phẳng
Hai đường thẳng a và b ở Hình 31b không cùng nằm trong một mặt phẳng.
Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.
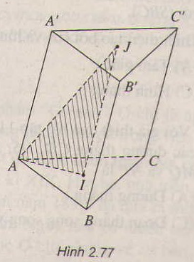
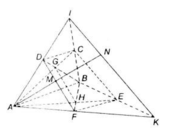
a) Trong (ABCD) : AC ∩ BD = I, Trong ( ABEF): AE ∩ BF = J
=> (ACE) ∩ (BDF) = IJ
Tương tự (BCE) ∩ ( ADF) = GH
b) Trong (AGH): AM ∩ GH = N, chứng minh N AM và N
(BCE)
c) Chứng minh bằng phương pháp phản chứng. Giả sử AC và BE cùng nằm trong một mặt phẳng, lập luận dẫn tới (ABCD) ≡ (ABEF), trái với giả thiết
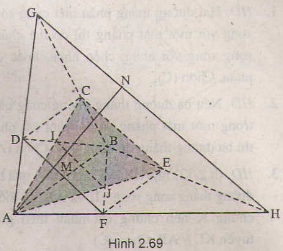
a) Giao tuyến của các cặp mặt phẳng
*Giao tuyến của (AEC) và (BFD)
• Trong hình thang ABCD, AC cắt DB tại G, ta có:
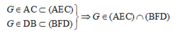
Tương tự, AE cắt BF tại H,
Ta có :
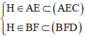⇒ H ∈ (AEC) ∩ (BFD).
Vậy GH = (AEC) ∩ (BFD)
*Giao tuyến của (BCE) và (ADF)
Trong hình thang ABCD, BC cắt AD tại I, ta có: I ∈ (BCE) ∩ (ADF)
Trong hình thang ABEF, BE cắt AF tại K, ta có: K ∈ (BCE) ∩ (ADF)
Vậy IK = (BCE) ∩ (ADF)
b) Giao điểm của AM với mp(BCE)
Trong mp(ADF), AM cắt IK tại N, ta có:
N ∈ IK ⊂ (BCE)
Vậy N = AM ∩ (BCE).
c) Giả sử AC cắt BF.
⇒ Qua AC và BF xác định duy nhất 1 mặt phẳng.
Mà qua A và BF có duy nhất mặt phẳng (ABEF)
⇒ AC ⊂ (ABEF)
⇒ C ∈ (ABEF) (Vô lý).
Vậy AC và BF không cắt nhau.
cắt nhau và song song