Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v=v_{tb}2=8.2=16\left(\frac{km}{gi\text{ờ}}\right)\)
\(\Rightarrow v_1+v_2=16\)
\(\Leftrightarrow12+v_2=16\Rightarrow v_2=4\left(\frac{km}{h}\right)\)

Thời gian người đi bộ đi được 1 vòng là :
\(v_1=\dfrac{s}{t_1}\Rightarrow t_1=\dfrac{s}{v_1}=\dfrac{1800}{1,5}=1200\left(s\right)\)
Trong thời gian 1200s người đi xe đạp đi được quãng đường là :
\(v_2=\dfrac{s}{t_1}\Rightarrow s=v_2.t_1=6.1200=7200\left(m\right)\)
Số vòng người đi xe đạp đi được cùng thời gian với người đi bộ là :
\(7200:1800=4\left(vòng\right)\)
Vậy khi người đi bộ đi được 1 vòng thì người đi bộ gặp người đi xe đạp 4 lần

\(\Rightarrow vtb=\dfrac{S}{\dfrac{\dfrac{1}{3}S}{25}+\dfrac{\dfrac{2}{3}S}{35}}=\dfrac{S}{\dfrac{S}{75}+\dfrac{2S}{105}}=\dfrac{S}{\dfrac{S\left(2.75+105\right)}{75.105}}=\dfrac{75.105}{2.75+105}=30,88km/h\)

\(v_{tb}=\dfrac{1}{\dfrac{\dfrac{1}{3}}{25}+\dfrac{\dfrac{2}{3}}{35}}\approx30,882\left(\dfrac{km}{h}\right)\)

\(v_{tb}=\dfrac{s}{\dfrac{\dfrac{1}{3}s}{42}+\dfrac{\dfrac{2}{3}s}{36}}=\dfrac{s}{\dfrac{s}{126}+\dfrac{2s}{108}}=\dfrac{s}{\dfrac{s\left(2\cdot126+108\right)}{126\cdot108}}=\dfrac{126\cdot108}{2\cdot126+108}=37,8\left(\dfrac{km}{h}\right)\)

ta có:
thời gian đi từ A dến B là:
t1=t2/1,5=1h
do vận tốc tỉ lệ nghịch với thời gian nên:
\(\frac{v+v'}{v-v'}=\frac{t_2}{t_1}=1,5\)
\(\Leftrightarrow v+v'=1,5\left(v-v'\right)\)
\(\Leftrightarrow v+v'=1,5v-1,5v'\)
\(\Leftrightarrow0,5v-2,5v'=0\)
\(\Leftrightarrow0,5v=2,5v'\)
\(\Rightarrow v=5v'\)
ta lại có:
S1+S2=2S
\(\Leftrightarrow1\left(v+v'\right)+1,5\left(v-v'\right)=2.48\)
\(\Leftrightarrow v+v'+1,5v-1,5v'=96\)
\(\Leftrightarrow2,5v-0.5v'=96\)
mà v=5v' nên:
2,5.5v'-0.5v'=96
\(\Rightarrow12v'=96\)
giải phương trình ta có:
v'=8km/h;v=40km/h
vận tốc trung bình của canô trong một lượt đi về là:
\(v_{tb}=\frac{2S}{t_1+t_2}=\frac{48.2}{1.5+1}=\frac{96}{2.5}=38.4\)

gọi:
t là thời gian dự định
ta có:
nếu xe đi với vận tốc 48km/h thì:
\(t=\frac{S}{48}+0.3\)
nếu xe đi với vận tốc 12km/h thì:
\(t=\frac{S}{12}-0.45\)
do thời gian dự định ko đổi nên:
\(\frac{S}{48}+0.3=\frac{S}{12}-0.45\)
giải phương trình ta có S=12km
tứ đó ta suy ra t=0.55h
b)ta có:
AC+BC=12
\(\Leftrightarrow v_1t_1+v_2t_2=12\)
\(\Leftrightarrow48t_1+12t_2=12\)
mà t1+t2=t=0.55
\(\Rightarrow48t_1+12\left(0.55-t_1\right)=12\)
giải phương trình ta có: t1=0.15h
từ đó ta suy ra AC=7.2km
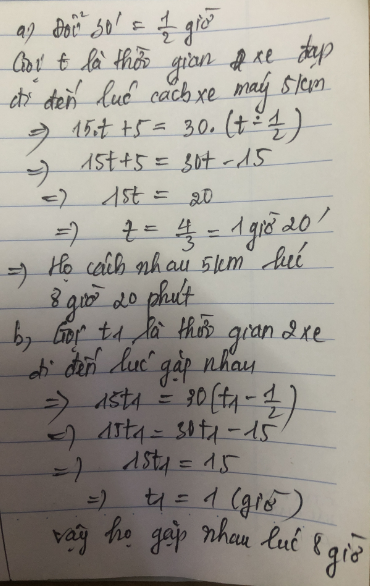


a) Gọi độ dài qđ là: s(km), s>0
Ô tô đi nửa qđ đầu mất: \(\dfrac{s}{\dfrac{2}{v_1}}=\dfrac{s}{2v_1}\)(h)
Ô tô đi nửa qđ sau mất: \(\dfrac{s}{\dfrac{2}{v_2}}=\dfrac{s}{2v_2}\)(h)
Vận tốc TB của ng đó trên cả qđ là: \(v_{tb}=\dfrac{s}{\dfrac{s}{2v_1}+\dfrac{s}{2v_2}}=\dfrac{2v_1v_2}{v_1+v_2}\)(km/h)
Vậy......
b) Gọi tổng thời gian ô tô đó chuyển động là t(h), t>0
Quãng đường ô tô đó đi đc trong nửa t.g đầu là: \(\dfrac{t}{2}.v_1\)(km)
Quãng đường ô tô đó đi đc trong nửa t.g sau là: \(\dfrac{t}{2}.v_2\)(km)
Vận tốc TB của ô tô đó là: \(v'_{tb}=\dfrac{\dfrac{t}{2}.v_1+\dfrac{t}{2}.v_2}{t}=\dfrac{v_1+v_2}{2}\)(km/h)
Vậy......
c) Ta có: \(v_{tb}-v'_{tb}=\dfrac{2v_1v_2}{v_1+v_2}-\dfrac{v_1+v_2}{2}=\dfrac{4v_1v_2}{2\left(v_1+v_2\right)}-\dfrac{\left(v_1+v_2\right)^2}{2\left(v_1+v_2\right)}\)
\(=\dfrac{4v_1v_2-\left(v_1+v_2\right)^2}{2\left(v_1+v_2\right)}=\dfrac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}\)
Vì \(\left\{{}\begin{matrix}\left(v_1-v_2\right)^2>0\\\left(v_1+v_2\right)>0\left(vì v_1, v_2>0\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\left(v_1-v_2\right)^2< 0\\2\left(v_1+v_2\right)>0\end{matrix}\right.\)
\(\Rightarrow\dfrac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}< 0\Rightarrow v_{tb}< v'_{tb}\)
Vậy.....