Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

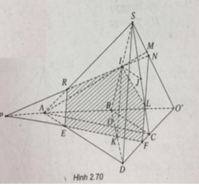
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
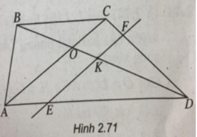
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do 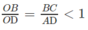 nên OB < OD. Do đó điểm K thuộc đoạn OD.
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.

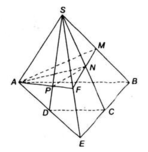
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
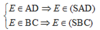
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

Kéo dài AD và BC cắt nhau tại E
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
Trong mp (SBC), nối MN kéo dài cắt SE tại F
Trong mp (SAD), nối AF cắt SD tại I
\(\Rightarrow I=SD\cap\left(AMN\right)\)
Tứ giác AINM chính là thiết diện của (AMN) và chóp
MN là đường trung bình tam giác SCD \(\Rightarrow F\) là trung điểm SE
Mặt khác CD song song và bằng 1/2 AB \(\Rightarrow\) CD là đường trung bình tam giác ABE hay D là trung điểm AE
\(\Rightarrow\) I là trọng tâm tam giác SAE
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{3}\)

\(SA=\left(SAC\right)\cap\left(SAD\right)\)
Trong mp (ABCD), nối CM kéo dài cắt DA kéo dài tại E
Trong mp (SAD), nối NE cắt SA tại H
\(\Rightarrow H=SA\cap\left(MNC\right)\)
Theo cách dựng trên ta có CM, AD, HN đồng duy tại E
Trong mp (ABCD), nối DM kéo dài cắt CB kéo dài tại F
\(\Rightarrow MN\) là đường trung bình tam giác SDF
\(\Rightarrow MN//SF\Rightarrow MN//\left(SBC\right)\)

a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)

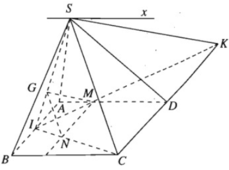
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
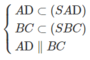
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
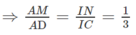
Mà 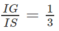
(G là trọng tâm của ∆SAB) nên
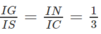 ⇒ GN // SC
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
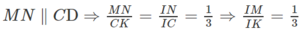
Ta có:
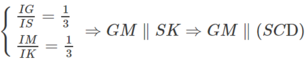

a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)


+ Ta tìm giao tuyến của mp (IBC) và (SAD)
+ Trong mặt phẳng (SAD) , gọi giao điểm của Ix và SD là J
⇒ IJ // BC.
Lại có; I là trung điểm của SA nên J là trung điểm của SD.
⇒ A và B đều đúng.
+ Giao tuyến của (IBC) và (SAD )là IJ.
Xét tam giác SAD có I và J lần lượt là trung điểm của SA và SD nên IJ là đường trung bình của tam giác
⇒ IJ // AD // BC mà BC ⊂ (SBC)
⇒ IJ // mp(SBC) nên C đúng
+ Ta tìm giao tuyến của mp (IBC) và (SAD)
+ Trong mặt phẳng (SAD) , gọi giao điểm của Ix và SD là J
⇒ IJ // BC.
Lại có; I là trung điểm của SA nên J là trung điểm của SD.
⇒ A và B đều đúng.
+ Giao tuyến của (IBC) và (SAD )là IJ.
Xét tam giác SAD có I và J lần lượt là trung điểm của SA và SD nên IJ là đường trung bình của tam giác
⇒ IJ // AD // BC mà BC ⊂ (SBC)
⇒ IJ // mp(SBC) nên C đúng