Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

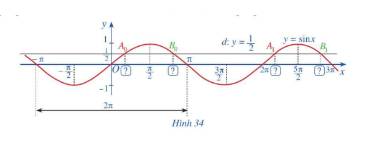
a) Hoành độ của \({A_0}\) là \(\frac{\pi }{6}\)
Hoành độ của \({B_0}\) là \(\frac{{5\pi }}{6}\)
b) Hoành độ của \({A_1}\) là \(\frac{{13\pi }}{6}\)
Hoành độ của \({B_1}\) là \(\frac{{17\pi }}{6}\)

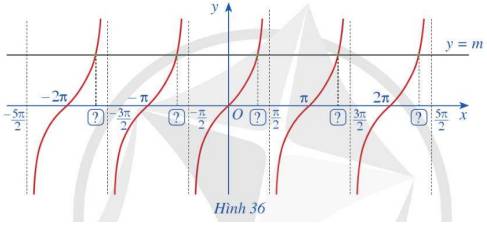
a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)

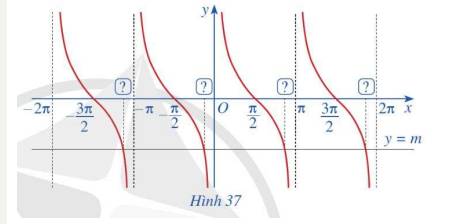
a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)

a)
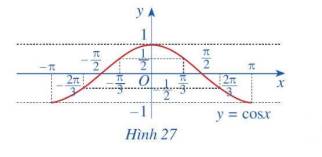
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
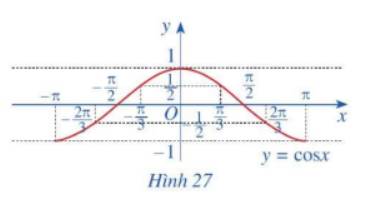
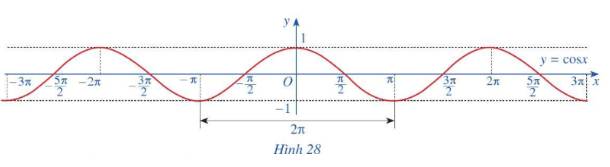
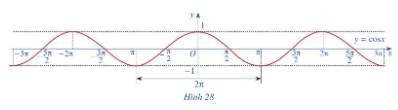
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.


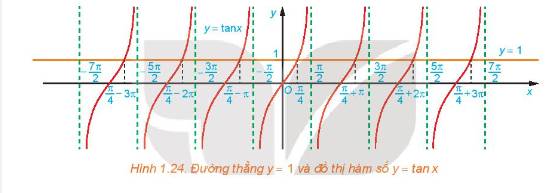
Theo đồ thì của hàm số \(y = \tan x\), số giao điểm của đường thẳng y=m với đồ thị hàm số \(y = \tan x\)trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là 1

Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)
\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow - 2\pi \le \frac{\pi }{4} + k\pi \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)
Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)
Vậy ta chọn đáp án A

a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Lời giải:
$y'=\frac{-1}{(x+1)^2}$
Giao điểm của đồ thị $y=\frac{x+2}{x+1}$ vớ trục hoành là $(-2,0)$
PTTT của $y=\frac{x+2}{x+1}$ tại điểm tiếp điểm $(-2,0)$ là:
$y=f'(-2)(x+2)+f(-2)=\frac{-1}{(-2+1)^2}(x+2)+0$
$y=-x-2$
Đường tiếp tuyến $y=-x-2$ cắt trục tung tại điểm có tung độ:
$y=-0-2=-2$

a)
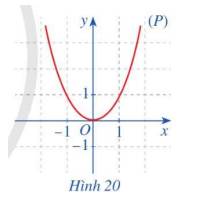
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
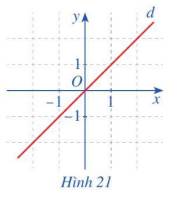
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d
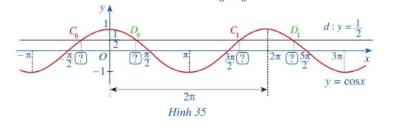

a) Hoành độ của \({C_0}\) là \( - \frac{\pi }{3}\)
Hoành độ của \({D_0}\) là \(\frac{\pi }{3}\)
b) Hoành độ của \({C_1}\) là \(\frac{{5\pi }}{3}\)
Hoành độ của \({D_1}\) là \(\frac{{7\pi }}{3}\)