Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\frac{5}{2}-3\left(\frac{1}{3}-x\right)=\frac{1}{4}-7x\)
\(\Leftrightarrow\frac{5}{2}-1+x=\frac{1}{4}-7x\)
\(\Leftrightarrow8x=-\frac{5}{4}\)
\(\Leftrightarrow x=-\frac{5}{32}\)
c)\(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x\left(x+1\right)}=\frac{2001}{2003}\)
\(\Leftrightarrow2\left(\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2001}{2003}\)
\(\Leftrightarrow\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{x\left(x+1\right)}=\frac{2001}{4006}\)
\(\Leftrightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{2001}{4006}\)
\(\Leftrightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{2001}{4006}\)
\(\Leftrightarrow\frac{1}{x+1}=\frac{1}{2003}\)
\(\Leftrightarrow x+1=2003\)
\(\Leftrightarrow x=2002\)

2, ta thấy:
\(\dfrac{2008}{2009}< \dfrac{2008}{2009+2010}\left(1\right)\)
\(\dfrac{2009}{2010}< \dfrac{2009}{2009+20010}\left(2\right)\)
từ (1) và (2) cộng vế với vế ta đc :\(\dfrac{2008}{2009}+\dfrac{2009}{20010}< \dfrac{2008}{2009+2010}+\dfrac{2009}{2009+2010}=\dfrac{2008+2009}{2009+2010}\)

Câu1:
a: \(=2008^2-\left(2008-2\right)\left(2008+2\right)\)
\(=2008^2-\left(2008^2-4\right)\)
=4
b: \(=\dfrac{23\cdot29\cdot10101}{23\cdot29\cdot10101}=1\)
c: \(=\dfrac{\left(2^{17}+5^{17}\right)\left(3^{14}-5^{12}\right)\cdot\left(16-16\right)}{15^2+5^3+67^7}\)
=0

Câu 1: Lời giải:
a, Đặt \(A=\dfrac{3x+7}{x-1}\).
Ta có: \(A=\dfrac{3x+7}{x-1}=\dfrac{3x-3+10}{x-1}=\dfrac{3x-3}{x-1}+\dfrac{10}{x-1}=3+\dfrac{10}{x-1}\)
Để \(A\in Z\) thì \(\dfrac{10}{x-1}\in Z\Rightarrow10⋮x-1\Leftrightarrow x-1\in U\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng sau:
| \(x-1\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(5\) | \(-5\) | \(10\) | \(-10\) |
| \(x\) | \(2\) | \(0\) | \(3\) | \(-1\) | \(6\) | \(-4\) | \(11\) | \(-9\) |
Vậy, với \(x\in\left\{-9;-4;-1;0;2;3;6;11\right\}\)thì \(A=\dfrac{3x+7}{x-1}\in Z\).
Câu 3:
a, Ta có: \(-\left(x+1\right)^{2008}\le0\)
\(\Rightarrow P=2010-\left(x+1\right)^{2008}\le2010\)
Dấu " = " khi \(\left(x+1\right)^{2008}=0\Rightarrow x+1=0\Rightarrow x=-1\)
Vậy \(MAX_P=2010\) khi x = -1
b, Ta có: \(-\left|3-x\right|\le0\)
\(\Rightarrow Q=1010-\left|3-x\right|\le1010\)
Dấu " = " khi \(\left|3-x\right|=0\Rightarrow x=3\)
Vậy \(MAX_Q=1010\) khi x = 3
c, Vì \(\left(x-3\right)^2+1\ge0\) nên để C lớn nhất thì \(\left(x-3\right)^2+1\) nhỏ nhất
Ta có: \(\left(x-3\right)^2\ge0\Rightarrow\left(x-3\right)^2+1\ge1\)
\(\Rightarrow C=\dfrac{5}{\left(x-3\right)^2+1}\le\dfrac{5}{1}=5\)
Dấu " = " khi \(\left(x-3\right)^2=0\Rightarrow x=3\)
Vậy \(MAX_C=5\) khi x = 3
d, Do \(\left|x-2\right|+2\ge0\) nên để D lớn nhất thì \(\left|x-2\right|+2\) nhỏ nhất
Ta có: \(\left|x-2\right|\ge0\Rightarrow\left|x-2\right|+2\ge2\)
\(\Rightarrow D=\dfrac{4}{\left|x-2\right|+2}\le\dfrac{4}{2}=2\)
Dấu " = " khi \(\left|x-2\right|=0\Rightarrow x=2\)
Vậy \(MAX_D=2\) khi x = 2

a.\(\dfrac{-4}{5}-\left(\dfrac{2}{3}x+1\dfrac{1}{4}\right)=\dfrac{2}{7}\)
\(\left(\dfrac{2}{3}x+1\dfrac{1}{4}\right)=\dfrac{-4}{5}-\dfrac{2}{7}=\dfrac{-38}{35}\)
\(\dfrac{2}{3}x=\dfrac{-38}{35}-1\dfrac{1}{4}\)
\(\dfrac{2}{3}x=\dfrac{-327}{140}\Rightarrow x=\dfrac{-327}{140}:\dfrac{2}{3}=\dfrac{-981}{280}\)
Vậy \(x=\dfrac{-981}{280}\)
b. \(\dfrac{5}{6}+\left(\dfrac{3}{4}-\dfrac{1}{2}:x\right)=\dfrac{-2}{3}\)
\(\left(\dfrac{3}{4}-\dfrac{1}{2}:x\right)=\dfrac{-2}{3}-\dfrac{5}{6}=\dfrac{-3}{2}\)
\(\dfrac{1}{2}:x=\dfrac{3}{4}-\dfrac{-3}{2}\)
\(\dfrac{1}{2}:x=\dfrac{9}{4}\Rightarrow x=\dfrac{1}{2}:\dfrac{9}{4}=\dfrac{2}{9}\)
Vậy \(x=\dfrac{2}{9}\)
c. \(\left(\dfrac{4}{5}x-1\dfrac{1}{3}\right):\dfrac{3}{4}=0,7\)
\(\left(\dfrac{4}{5}x-1\dfrac{1}{3}\right)=0,7.\dfrac{3}{4}=\dfrac{21}{40}\)
\(\dfrac{4}{5}x=\dfrac{21}{40}+1\dfrac{1}{3}=\dfrac{223}{120}\)
\(\Rightarrow x=\dfrac{223}{120}:\dfrac{4}{5}=\dfrac{223}{96}\)
Vậy \(x=\dfrac{223}{96}\)
d. \(\dfrac{5}{6}-\dfrac{3}{4}x=1\dfrac{1}{3}+0,5x\)
\(0,5x+\dfrac{3}{4}x=\dfrac{5}{6}-1\dfrac{1}{3}\)
\(\dfrac{5}{4}x=\dfrac{-1}{2}\Rightarrow x=\dfrac{-1}{2}:\dfrac{5}{4}=\dfrac{-2}{5}\)
Vậy \(x=\dfrac{-2}{5}\)

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 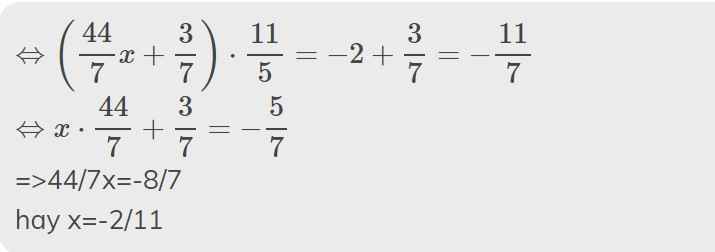
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

Bài 1:
a) \(\dfrac{2}{5}\cdot x-\dfrac{1}{4}=\dfrac{1}{10}\)
\(\dfrac{2}{5}\cdot x=\dfrac{1}{10}+\dfrac{1}{4}\)
\(\dfrac{2}{5}\cdot x=\dfrac{7}{20}\)
\(x=\dfrac{7}{20}:\dfrac{2}{5}\)
\(x=\dfrac{7}{8}\)
Vậy \(x=\dfrac{7}{8}\).
b) \(\dfrac{3}{5}=\dfrac{24}{x}\)
\(x=\dfrac{5\cdot24}{3}\)
\(x=40\)
Vậy \(x=40\).
c) \(\left(2x-3\right)^2=16\)
\(\left(2x-3\right)^2=4^2\)
\(\circledast\)TH1: \(2x-3=4\\ 2x=4+3\\ 2x=7\\ x=\dfrac{7}{2}\)
\(\circledast\)TH2: \(2x-3=-4\\ 2x=-4+3\\ 2x=-1\\ x=\dfrac{-1}{2}\)
Vậy \(x\in\left\{\dfrac{7}{2};\dfrac{-1}{2}\right\}\).
Bài 2:
a) \(25\%-4\dfrac{2}{5}+0.3:\dfrac{6}{5}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{3}{10}:\dfrac{6}{5}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{3}{10}\cdot\dfrac{5}{6}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{1}{4}\)
\(=\dfrac{5}{20}-\dfrac{88}{20}+\dfrac{5}{20}\)
\(=\dfrac{5-88+5}{20}\)
\(=\dfrac{78}{20}=\dfrac{39}{10}\)
b) \(\left(\dfrac{1}{6}-\dfrac{1}{5^2}\cdot5+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{1}{6}-\dfrac{1}{25}\cdot5+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{1}{6}-\dfrac{1}{5}+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{5}{30}-\dfrac{6}{30}+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{5-6+1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=0\cdot\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=0\)
Bài 3:
a) \(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)\)
\(=\dfrac{-3}{7}\cdot1\)
\(=\dfrac{-3}{7}\)
b) \(7\dfrac{5}{9}-\left(2\dfrac{3}{4}+3\dfrac{5}{9}\right)\)
\(=\dfrac{68}{9}-\dfrac{11}{4}-\dfrac{32}{9}\)
\(=\dfrac{68}{9}-\dfrac{32}{9}-\dfrac{11}{4}\)
\(=4-\dfrac{11}{4}\)
\(=\dfrac{16}{4}-\dfrac{11}{4}\)
\(\dfrac{5}{4}\)
Bài 4:
\(\dfrac{4}{12\cdot14}+\dfrac{4}{14\cdot16}+\dfrac{4}{16\cdot18}+...+\dfrac{4}{58\cdot60}\)
\(=2\left(\dfrac{1}{12\cdot14}+\dfrac{1}{14\cdot16}+\dfrac{1}{16\cdot18}+...+\dfrac{1}{58\cdot60}\right)\)
\(=2\left(\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{18}+...+\dfrac{1}{58}-\dfrac{1}{60}\right)\)
\(=2\left(\dfrac{1}{12}-\dfrac{1}{60}\right)\)
\(=2\left(\dfrac{5}{60}-\dfrac{1}{60}\right)\)
\(=2\cdot\dfrac{1}{15}\)
\(=\dfrac{2}{15}\)