Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 :
\(\hept{\begin{cases}3x+2y=11\left(1\right)\\x+2y=5\left(2\right)\end{cases}}\)
Lấy phương trình (1) - phương trình (2) ta được :
\(2x=6\Leftrightarrow x=3\)
Thay x = 3 vào phương trình (2) ta được :
\(3+2y=5\Leftrightarrow2y=2\Leftrightarrow y=1\)
Vậy \(\left(x;y\right)=\left(3;1\right)\)

a, \(\hept{\begin{cases}4x-y=7\\x+3y=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x-7\left(1\right)\\x+3y=5\left(2\right)\end{cases}}\)
Thế (1) vào (2) ta được : \(x+3\left(4x-7\right)=5\Leftrightarrow x+12x-21=5\)
\(\Leftrightarrow13x=26\Leftrightarrow x=2\)
Theo (1) ta có : \(y=8-7=1\)
Vậy \(\left(x;y\right)=\left(2;1\right)\)

Bài 1:
a: 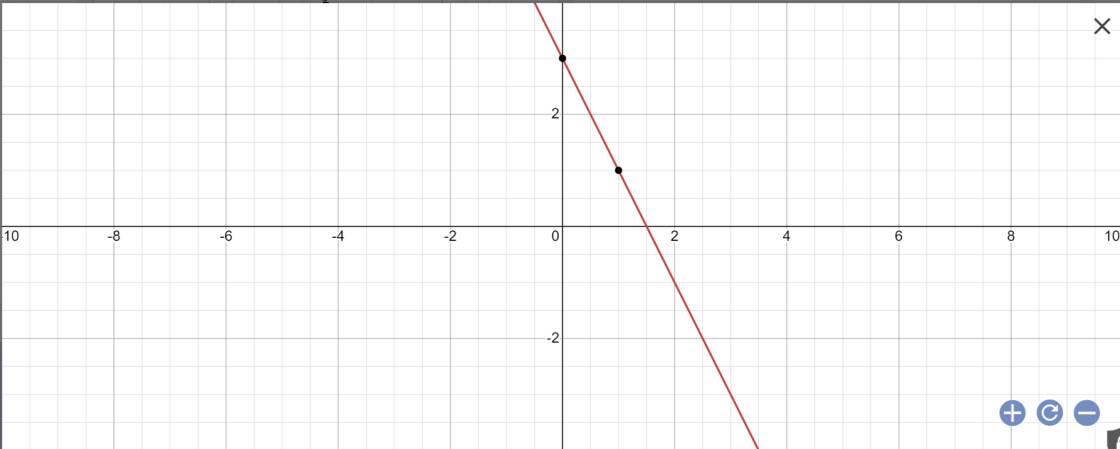
b: Vì (d')//(d) nên \(\left\{{}\begin{matrix}a=-2\\b< >3\end{matrix}\right.\)
vậy: (d'): y=-2x+b
Thay x=2 và y=0 vào (d'), ta được:
\(b-2\cdot2=0\)
=>b-4=0
=>b=4
Vậy: (d'): y=-2x+4






Trả lời:
a. xác định a,b:
vì đồ thị hàm số y=ax+b // đường y=-1/2x+2020
=> a=-1/2
Đồ thị cắt trục hoành tại điểm có tọa độ(-5,0), thay vào ta có:
0= -1/2.-5 +b => b=-5/2
Đường thẳng d là: y=-1/2 x-5/2
Vì đường thẳng ( d ) : y = ax +b song song với đường thẳng
\(y=-\frac{1}{2}x+2020\Leftrightarrow\)\(\hept{\begin{cases}a=-\frac{1}{2}\\be2020\end{cases}}\)
khi đó phương trình đường thẳng ( d ) có dạng ( d ) :\(y=-\frac{1}{2}x+b,\)với \(be2020\)
Vì ( d ) cắt trục hoành tại điểm có hoành độ bằng -5 nên đường thẳng ( d ) đi qua điểm ( - 5 ; 0 )
thay tọa độ điểm ( - 5 ; 0 )và phương trình đường thẳng ( d ) ta có :
\(0=-\frac{1}{2}\times\left(-5\right)+b\)
\(\Leftrightarrow0=\frac{5}{2}+b\)
\(\Leftrightarrow b=-\frac{5}{2}\)thỏa mãn
Vậy \(a=-\frac{1}{2}\)và \(b=-\frac{5}{2}\)
bình chọn em với