Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nếu ta dùng cách rút gọn biểu thức thì ta có kết quả
A=(8a-8)x2+(2a-2)x-15a+15
còn nếu sử dụng cách Phân tích thành nhân tử thì ta sẽ có kết quả là
A=(a-1)(2x+3)(4x-5)
(tự xét )
B = (7x - 6y)×(4x + 3y) - 2×(14x + y)×(x - 9y) - 19×(13xy - 1)
= 28x^2 - 24xy + 21xy - 18y^2 - 2.(14x^2 + xy - 126xy - 9y^2) - 247xy + 19
= 28x^2 - 24xy + 21xy - 18y^2 - 28x^2 - 2xy + 252xy + 18y^2 - 247xy + 19
= 19
vậy biểu thức A ko phụ thuộc vào x, y
hc tốt
tớ chỉ biết làm phần B thôi
B= (7x - 6y)×(4x + 3y) - 2×(14x + y)×(x - 9y) - 19×(13xy - 1)
= 28x^2 - 24xy + 21xy - 18y^2 - 2.(14x^2 + xy - 126xy - 9y^2) - 247xy + 19
= 28x^2 - 24xy + 21xy - 18y^2 - 28x^2 - 2xy + 252xy + 18y^2 - 247xy + 19
= 19
vậy biểu thức A ko phụ thuộc vào x, y
phần A tương tự


a) 4x2 - 2x + 3 - 4x.(x - 5) = 7x - 3
--> 4x2 - 2x + 3 - 4x2 + 20x = 7x - 3
--> 4x2 - 2x - 4x2 + 20x - 7x = -3 - 3
--> 11x = -6
--> x = \(\frac{-6}{11}\)
b) -3x.(x - 5) + 5.(x - 1) + 3x2 = 4x
--> -3x2 + 15x + 5x - 5 + 3x2 = 4x
--> -3x2 + 15x + 5x + 3x2 - 4x = 5
--> 16x = 5
--> x = \(\frac{5}{16}\)
c) 7x.(x - 2) - 5.(x - 1) = 21x2 - 14x2 + 3
--> 7x2 - 14x - 5x + 5 = 7x2 + 3
--> 7x2 - 14x - 5x - 7x2 = -5 + 3
--> -19x = -2
--> x = \(\frac{2}{19}\)
d) 3.(5x - 1) - x.(x - 2) + x2 - 13x = 7
--> 15x - 3 - x2 + 2x + x2 - 13x = 7
--> 15x - x2 + 2x + x2 - 13x = 3 + 7
--> 4x = 10
--> x = \(\frac{5}{2}\)
e) \(\frac{1}{5}\)x.(10x - 15) - 2x.(x - 5) = 12
--> 2x2 - 3x - 2x2 + 10x = 12
--> 7x = 12
--> x = \(\frac{12}{7}\)
~ Học tốt ~

a) 4x2 - 2x + 3 - 4x(x - 5) = 7x - 3
=> 4x2 - 2x + 3 - 4x2 + 20x = 7x - 3
=> 18x + 3 = 7x - 3
=> 18x - 7x = -3 - 3
=> 11x = -6
=> x = -6/11
b) -3x(x - 5) + 5(x - 1) + 3x2 = 4x
=> -3x2 + 15x + 5x - 5 + 3x2 = 4x
=> 20x - 5 = 4x
=> 20x - 4x = 5
=> 16x = 5
=> x = 5/16
\(c,7x\left(x-2\right)-5\left(x-1\right)=21x^2-14x^2+3\)
\(\Leftrightarrow7x^2-14x-5x+5=7x^2+3\)
\(\Leftrightarrow7x^2-7x^2-19x=3-5\)
\(\Leftrightarrow-19x=-2\)
\(\Leftrightarrow x=\frac{2}{19}\)

Bài 2:
a: \(\Leftrightarrow4x^2-14x+10x-35-\left(4x+3\right)^2=16\)
\(\Leftrightarrow4x^2-4x-35-16x^2-24x-9-16=0\)
\(\Leftrightarrow-12x^2-28x-60=0\)
\(\Leftrightarrow3x^2+7x+15=0\)
\(\text{Δ}=7^2-4\cdot3\cdot15=-131< 0\)
Do đó: Phương trình vô nghiệm
b: Ta có: \(\left(8x^2+3\right)\left(8x^2-3\right)-\left(8x^2-1\right)^2=22\)
\(\Leftrightarrow64x^4-9-64x^4+16x^2-1=22\)
\(\Leftrightarrow16x^2=32\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
c: Ta có: \(49x^2+14x+1=0\)
=>\(\left(7x+1\right)^2=0\)
hay x=-1/7

Bài 2:
a: \(\Leftrightarrow4x^2-14x+10x-35-\left(4x+3\right)^2=16\)
\(\Leftrightarrow4x^2-4x-35-16x^2-24x-9-16=0\)
\(\Leftrightarrow-12x^2-28x-60=0\)
\(\Leftrightarrow3x^2+7x+15=0\)
\(\text{Δ}=7^2-4\cdot3\cdot15=-131< 0\)
Do đó: Phương trình vô nghiệm
b: Ta có: \(\left(8x^2+3\right)\left(8x^2-3\right)-\left(8x^2-1\right)^2=22\)
\(\Leftrightarrow64x^4-9-64x^4+16x^2-1=22\)
\(\Leftrightarrow16x^2=32\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
c: Ta có: \(49x^2+14x+1=0\)
=>\(\left(7x+1\right)^2=0\)
hay x=-1/7

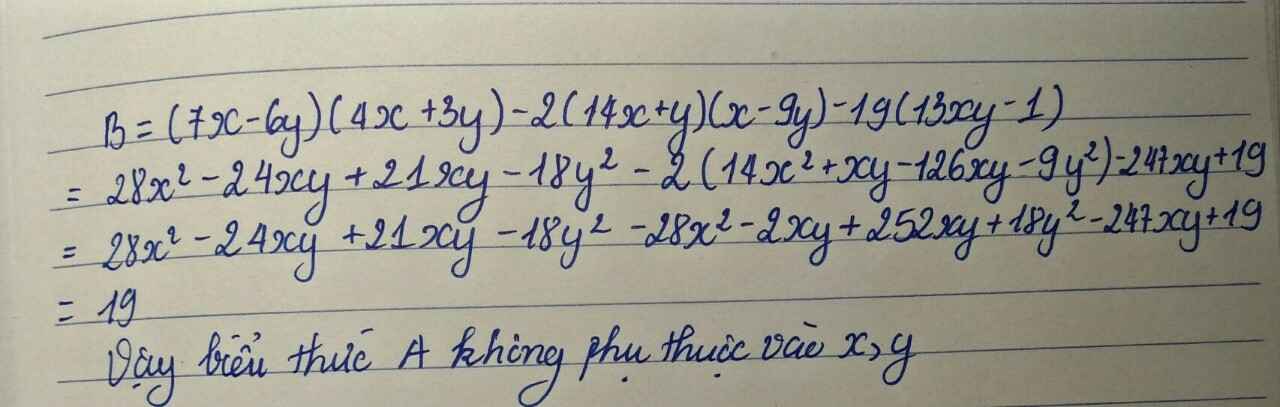
Đề?
chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x