Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

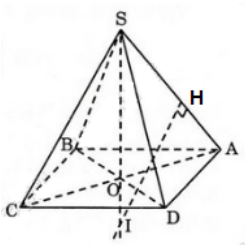
Qua O vẽ đường thẳng d vuông góc với (ABCD)
Khi đó d là trục đường tròn ngoại tiếp hình vuông ABCD
Gọi H là trung điểm của cạnh SA
Trong mặt phẳng (SAO) đường trung trực của đoạn SA cắt đường thẳng SO tại I , ta có: \(\Delta SAO\) đòng dạng \(\Delta SIH\)
\(\Rightarrow\dfrac{SA}{SO}=\dfrac{SI}{SH}\Leftrightarrow SI=\dfrac{SA.SH}{SO}=\dfrac{SA^2}{2SO}\)
Mà \(SA^2=SO^2+OA^2=\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{3a^2}{4}\)
\(\Leftrightarrow SA=\dfrac{a\sqrt{3}}{2}\)
Khi đó \(SI=\dfrac{3a^2}{\dfrac{4}{2.\dfrac{a}{2}}}=\dfrac{3a}{4}\)
Mặt khác \(\left\{{}\begin{matrix}IS=IA\\IA=IB=IC=ID\end{matrix}\right.\)
\(\Rightarrow IS=IA=IB=IC=ID=\dfrac{3a}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là I và bán kính \(R=SI=\dfrac{3a}{4}\)
Diện tích mặt cầu là: \(S=4\pi R^2=4\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{4}\)
Thể tích khối cầu là: \(V=\dfrac{4}{3}\pi R^2=\dfrac{4}{3}\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{16}\)

kẻ CE//BD ( E thuộc AD)
=> d( BD;SC)= d( BD; ( SCE))=d( O; ( SCE))
kẻ OK _|_SC
OC_|_ CE
SO_|_CE => CE_|_ ( SOC) => CE_|_OK
do đó OK_|_(SCE)=> d(O;(SCE))=OK
1/OK^2=1/SO^2+1/OC^2
câu 2:
BC//AD=> d( BC;SA)=d(BC:(SAD))=d( B;( SAD))=2 d( O; (SAD))
kẻ OH_|_ AD
kẻ OE_|_SH
ta có OH_|_AD; SO_|_AD=> AD_|_(SOH)=> AD_|_ OE
do đó OE_|_( SAD)=> d( O; (SAD))=OE

a) Vì I là trọng tâm của tam giác ABD nên \(AI=\dfrac{1}{3}AC\)


S B M H A E N C D
Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??

S M H G N A O D C
Ta có \(\begin{cases}BC\perp SA\\BC\perp AB\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\)\(\Rightarrow BC\perp AM\) (vì \(AM\subset\left(SAB\right)\left(1\right)\)
Mặt khác \(SC\perp\alpha\Rightarrow SA\perp AM\) (vì \(AM\subset\alpha\)) (2)
Từ (1) và (2) suy ra \(AM\perp\left(SBC\right)\Rightarrow AM\perp MG\) (vì \(MG\subset\left(SBC\right)\))
\(\Rightarrow\Delta AMG\) vuông tại M, tương tự ta cũng có tam giác ANG vuông tại N \(\Rightarrow\) tâm H đường tròn đáy của (H) là trung điểm AG, có bán kính \(R=\frac{AG}{2}\)
Xét tam giác vuông SAC tại A có \(AG=\frac{SA.AC}{SC}=\frac{\sqrt{6}}{3}a\Rightarrow R=\frac{\sqrt{6}}{6}a\)
Vì OH là đường cao (H)\(\Rightarrow OH\perp\alpha\Rightarrow OH\)//\(SC\Rightarrow O\) là giao điểm hai đường chéo AC, BD
\(\Rightarrow OH=\frac{1}{2}CG\).
Xét tam giác vuoongSAC có AG là đường cao, nên \(CG=\frac{AC^2}{SC}=\frac{2}{\sqrt{3}}a\Rightarrow OH=\frac{\sqrt{3}}{3}a\)
Vậy thể tích hình nón là \(V_{\left(H\right)}=\frac{1}{3}\pi.R^2.OH=\frac{\sqrt{3}}{54}\pi a^3\)




ko sao ô ơi, cứ đưa lên đi, mai tui đăng lại cx dc
Cách tính bài này đơn giản là tọa độ hóa nó (tứ diện cần tính ko đặc biệt, nhưng chóp ban đầu thì tọa độ hóa được), gọi A là gốc (0,0,0), quy ước a là 1 đơn vị độ dài, các tia AS, AB, AD lần lượt là Oz, Oy, Ox, ta có các tọa độ \(S\left(0,0,1\right)\); M(1,0,0), D(2,0,0), C(2,1,0), \(I\left(x;y;z\right)\) là tâm
\(SI=CI=DI=MI\Rightarrow\left\{{}\begin{matrix}x^2+y^2+\left(z-1\right)^2=\left(x-1\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+\left(y-1\right)^2+z^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-z=0\\4x-2z=3\\4x+2y-2z=4\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{3}{2};\dfrac{1}{2};\dfrac{3}{2}\right)\)
\(\Rightarrow R=SI=\dfrac{\sqrt{11}}{2}\)
Do quy ước a là 1 đơn vị độ dài nên đáp án chính xác là \(R=\dfrac{a\sqrt{11}}{2}\)
Lý do đáp án chỉ có số mà thiếu a: theo tư duy của mình thì người ra đề mang hướng giải y như mình bên trên, tức là quy ước độ dài rồi tọa độ hóa, nhưng khi đưa ra đáp án cuối cùng lại quên chuyển từ quy ước về đơn vị thực nên thiếu a. Về cơ bản là người ta quên, ko có gì bí ẩn đáng suy nghĩ ở đây cả :D. Kích thước là a thì mọi kích thước độ dài sẽ phụ thuộc a.