Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo trục Ox, tọa độ của Mx là: x = v0.t cũng chính là hoành độ của điểm M chuyển động ném ngang.
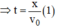
Tại thời điểm t, điểm M có tung độ (tọa độ của My):
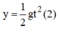
Thế (1) vào (2)
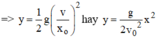
Thời gian chuyển động bằng thời gian rơi tự do của vật được thả từ cùng độ cao:
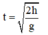
Tầm ném xa:
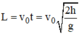

a) Vận tốc ban đầu của vật v 0 = v x .
Tại thời điểm t = 2s: v y = gt = 10.2 = 20m/s.
Mặt khác ta biết rằng: tan α = v y v x = t g 30 0 = 3 3 ⇒ v 0 = v x = 20 3 m / s
b) Thời gian chuyển động t = 2 h g = 2 . 65 10 = 3 , 6 s .
c) Tầm bay xa: x m a x = v 0 t = 20 3 . 3 , 6 = 124 , 56 m

a. Thời gian rơi của vật là:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.20}{10}}=2\) (s)
Tầm ném xa của vật là:
\(L=v_ot=10.2=20\) (m)
b. Vận tốc của vật khi chạm đất theo phương ngang và phương thẳng đứng lần lượt là:
\(v_x=v_0=10\) (m/s)
\(v_y=gt=10.2=20\) (m/s)
Vận tốc của vật khi chạm đất là:
\(v=\sqrt{v_x^2+v^2_y}=\sqrt{10^2+20^2}=22,36\) (m/s)

a) Vận tốc ban đầu của vật vo = vx.
Tại thời điểm t = 2s: vy = gt = 10.2 = 20m/s.


Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng lên, chọn mặt đất làm vật mốc
a. Ox: v0x=v=30m/s ; ax=0
Oy: v0Y=0 ; ay=-g=-10 m/s2
Ta có: x=v0X.t=30t \(\Leftrightarrow t=\dfrac{x}{30}\)
y=\(y_0+\dfrac{1}{2}at^2\)=\(y_0-\dfrac{1}{2}gt^2\) \(=80-\dfrac{1}{2}.10.\dfrac{x^2}{30^2}\)
\(\Leftrightarrow y=80-\dfrac{1}{180}x^2\)
Có : \(y=80-\dfrac{1}{2}.10.t^2\), thay y=0 ta được: t=4 (s)
Vậy thời gian kể từ lúc ném đến lúc chạm đất là 4(s)
c. Tầm xa của vật là: L=x=v0X.t=30.4=120 (m)

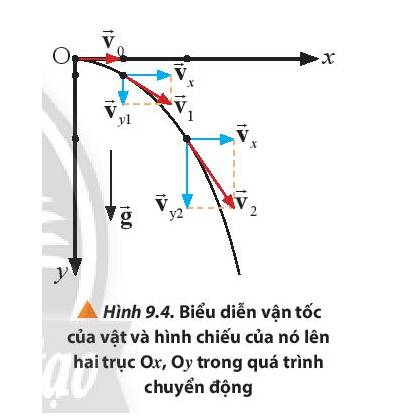
Xét chuyển động ném ngang trong mặt phẳng, vật luôn có gia tốc rơi tự do \(\overrightarrow g \) thẳng đứng hướng xuống và vuông góc với vận tốc ban đầu \(\overrightarrow {{v_0}} \)
Chọn hệ trục tọa độ Oxy như Hình 9.4, gốc thời gian là lúc thả vật
* Trên trục Ox:
- Gia tốc: ax = 0 nên vật chuyển động thẳng đều trên Ox.
- Vận tốc: vx = v0 là hằng số.
- Phương trình chuyển động: x = v0 .t.
* Trên trục Oy:
- Gia tốc: ay = g là hằng số nên vật chuyển động nhanh dần đều trên Oy
- Vận tốc: vy = g.t
- Phương trình chuyển động: \(y = \frac{1}{2}g{t^2}\)




\(t_r=\sqrt{\dfrac{2h}{g}}\)
\(L=v_0.t=v_0.\sqrt{\dfrac{2h}{g}}\)
\(v_{cđ}=\sqrt{v_x^2+v_y^2}\)
\(v_x=v_0;v_y=g.t\)
Pt tọa độ
\(x=v_0.t;y=\dfrac{1}{2}g.t^2\)
Pt quỹ đạo \(y=\dfrac{1}{2}g.\dfrac{x^2}{v_0^2}\)