Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!

Đáp án: C
HD Giải:
Theo tính thuận nghich của đường truyền sáng ta có:
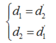
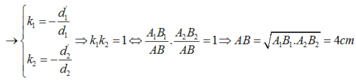
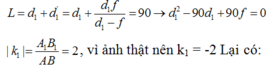
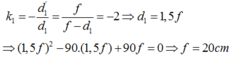


b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép nên:
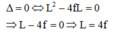
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm nên:
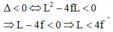

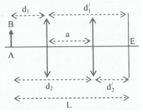
+ Theo tính thuận nghịch của chiều truyền ánh sáng 
@ Ta có thể giải cách khác như sau:
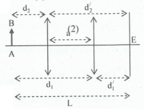

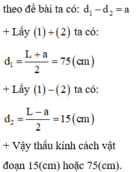

Đáp án cần chọn là: B
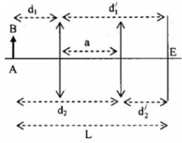
Theo tính thuận nghịch của chiều truyền ánh sáng, ta có: d 1 = d 2 ' d 2 = d 1 '
Ta có: d 1 + d 1 ' = L d 1 ' − d 1 = a → d 1 = L − a 2 d 1 ' = L + a 2
Mặt khác, ta có:
1 f = 1 d 1 + 1 d 1 ' = 2 L − a + 2 L + a
↔ 1 f = 2 72 − 48 + 2 72 + 48
→ f = 10 c m

Đáp án: C
HD Giải:
Theo tính thuận nghịch của đường truyền sáng ta có:
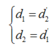
Ta có:
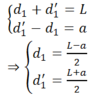
Ta lại có:
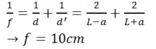

Sơ đồ tạo ảnh:

Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|

a) Để có 2 vị trí của TK cho ảnh rõ nét trên màn thì (*) có hai nghiệm dương phân biệt. Tức là
![]()
b) Để có 1 vị trí qua thấu kính cho ảnh rõ nét trên màn thì (*) có một nghiệm kép. Tức là
![]()
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì (*) vô nghiệm. Tức là
![]()
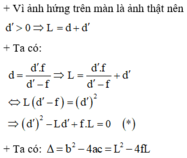

\(d+d'=160\)
\(\dfrac{d'}{d}=9\Rightarrow d'-9d=0\)
\(\left\{{}\begin{matrix}d+d'=160\\d'-9d=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}d'=144\left(cm\right)\\d=16\left(cm\right)\end{matrix}\right.\)
\(f=\dfrac{dd'}{d+d'}=\dfrac{144.16}{144+16}=14,4\left(cm\right)\)