Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với (x-2)!=1*2*3*...*(x-2)
Với 2-x cx phân tích vậy.
Vì x+2=2+x
=>(x+2)!=(2+x)! (phân tích như trên)

Bạn chỉ cần phân tích nó ra thành thừa số nguyên tố là xong

Ý bạn là sao nhỉ?
Theo mình hiểu thì bạn muốn biến 72 thành căn đúng không? Vậy thì bạn chỉ cần biểu diễn $72=\sqrt{72^2}=\sqrt{5184}$ thôi.

\(15\sqrt{\dfrac{1}{5}}=\dfrac{15}{\sqrt{5}}=3\sqrt{5}\)

`a(a+6)+10>0`
`<=>a^2+6a+10>0`
`<=>a^2+6a+9+1>0`
`<=>(a+3)^2+1>0` luôn đúng

Lời giải:
Nói đơn giản thế này. Khi đề cho: Cho đồ thị hàm số $y=x+2$
- Hàm số: chính là $y=x+2$, biểu diễn mối quan hệ giữa biến $x$ và biến $y$. Hàm số hiểu đơn giản giống như phép biểu diễn mối quan hệ giữa hai biến.
- Đồ thị hàm số (hay đồ thị): Khi có hàm số rồi, người ta muốn biểu diễn nó trên mặt phẳng tọa độ ra được 1 hình thù nào đó thì đó là đồ thị hàm số. Ví dụ, đths $y=x+2$ có dạng như thế này:
- Tọa độ giao điểm của hai đồ thị: Khi ta vẽ được đồ thị trên mặt phẳng tọa độ, 2 đồ thị đó giao nhau ở vị trí nào thì đó chính là tọa độ giao điểm. Ví dụ, trên mp tọa độ ta có 2 đồ thị $y=-2x+3$ và $y=x+6$ chả hạn. Điểm $A$, có tọa độ $(-1,5)$ chính là giao điểm. Như vậy, $(-1,5)$ là tọa độ giao điểm.
- Nhìn hình vẽ của đồ thị chỉ giúp ta có cái nhìn trực quan hơn. Khi muốn tìm giao điểm của 2 đồ thị hàm số, người ta thường dùng hàm số để tìm cho nhanh, vì hàm số biểu diễn mối quan hệ giữa hai biến một cách "số hóa" hơn.
- Với nhiều hàm số trở lên thì ta cứ xét từng cặp 1 thôi.
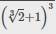 mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
\(5x^2+14x-432\)
\(=\left(5x^2+54x\right)-\left(40x+432\right)\)
\(=x\left(5x+54\right)-8\left(5x+54\right)\)
\(=\left(5x+54\right)\left(x-8\right)\)
#kễnh