Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để xác định được bán kính ta cần xác định được tâm của đường tròn chứa chi tiết máy này. Ta xác định tâm như sau:
+ Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
+ Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D. Khi đó D là tâm cần xác định.
+ Bán kính đường tròn cần tìm là độ dài đoạn DB (hoặc DA hoặc DC).
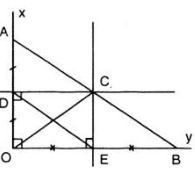
Ta có hình vẽ minh họa
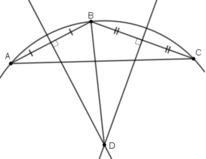

Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

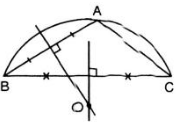
Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực này cắt nhau tại O.
Khi đó; OA = OB = OC
Suy ra: O là tâm của đường viền.

Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD

Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A

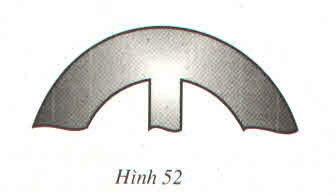
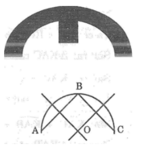
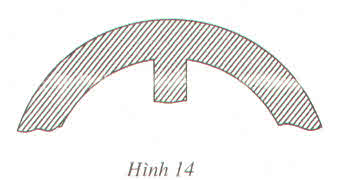
- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.

a) Gọi A là số tiền mua 5kg táo và 8kg nho
Ta có: A = 5x + 8y
b) Mỗi hộp táo có 12 kg nên 10 hộp có 10.12 = 120kg.
Mỗi hộp nho có 10 kg nên 15 hộp có 10.15 = 150kg.
Ta có: B = 120x + 150y
Các biểu thức A; B đều là đa thức.
a﴿ Gọi A là số tiền mua 5kg táo và 8kg nho
Ta có: A = 5x + 8y
b﴿ Mỗi hộp táo có 12 kg nên 10 hộp có 10.12 = 120kg.
Mỗi hộp nho có 10 kg nên 15 hộp có 10.15 = 150kg.
Ta có: B = 120x + 150y
Các biểu thức A; B đều là đa thức.

- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.




xem rùi