
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{x+1}{5}=\frac{-10}{16}\Rightarrow x+1=\frac{5.\left(-10\right)}{16}=\frac{-25}{8}\Rightarrow x=\frac{-25}{8}-1=-\frac{33}{8}\)
\(x+\frac{4}{5.9}+\frac{4}{9.13}+\frac{4}{13.17}+...+\frac{4}{41.45}=\frac{-37}{45}\)
\(x+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\frac{1}{13}-\frac{1}{17}+...+\frac{1}{41}-\frac{1}{45}=\frac{-37}{45}\)
\(x+\frac{1}{5}-\frac{1}{45}=\frac{-37}{45}\)
\(x+\frac{8}{45}=\frac{-37}{45}\)
\(x=\frac{-37}{45}-\frac{8}{45}\)
\(x=-1\)


\(x^2=3+5+2\sqrt{15}=8+\sqrt{60}\)
\(y^2=2+6+2\sqrt{12}=8+\sqrt{48}\)
Mà \(60>48\Rightarrow\sqrt{60}>\sqrt{48}\Rightarrow8+\sqrt{10}>8+\sqrt{48}\)
\(\Rightarrow x^2>y^2\Rightarrow x>y\) (do x;y đều dương)

Đáp án\(\frac{300}{10}\)mới là đáp án chính xác nha!!!

Ta có : \(\frac{x}{5}=\frac{y}{7}=\frac{z}{3}\)
\(\Rightarrow\left(\frac{x}{5}\right)^2=\left(\frac{y}{7}\right)^2=\left(\frac{z}{3}\right)^2=\frac{x^2}{5^2}=\frac{y^2}{7^2}=\frac{z^2}{3^2}\)\(=\frac{x^2}{25}=\frac{y^2}{49}=\frac{z^2}{9}=\frac{x^2+y^2-z^2}{25+49-9}=\frac{585}{65}=9\)
\(\Rightarrow x=9.5=45\)
\(y=9.7=63\)
\(z=9.3=27\)

có nhiều cách vd
x+y=4 và |2x+1|+|y-x|=5
vì x+y=4 =>x=4-y => |2(4-y)+1|+|y-(4-y)|=5 => |9-2y|+|2y-4|=5; Dâú "="xảy ra khi: |9-2y|+|2y-4| >=|9-2y+2y-4|=5 => (9-2y)(2y-4)>=0
=>9-2y>=0 và 2y-4>=0 hoặc 9-2y<=0 và 2y-4<=0
đến dây bn tự hiểu nhé

a) Ta có \(\hept{\begin{cases}\left(x-2y\right)^2\ge0\forall x;y\\\left(y+1\right)^6\ge0\forall y\end{cases}}\Rightarrow\left(x-2y\right)^2+\left(y+1\right)^6\ge0\forall x;y\)
=> (x - 2y)2 + (y + 1)6 = 0
<=> \(\hept{\begin{cases}x-2y=0\\y+1=0\end{cases}}\Rightarrow\hept{\begin{cases}x=2y\\y=-1\end{cases}}\Rightarrow\hept{\begin{cases}x=-2\\y=-1\end{cases}}\)
b) \(\left(\frac{2x}{3}\right)^2+10x=0\)
=> \(\frac{4x^2}{9}+10x=0\)
=> \(x\left(\frac{4x}{9}+10\right)=0\)
=> \(\orbr{\begin{cases}x=0\\\frac{4x}{9}+10=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\\frac{4x}{9}=-10\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-22,5\end{cases}}\)
Vậy \(x\in\left\{0;-22,5\right\}\)

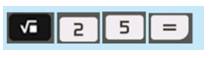
a) Kết quả trên màn hình là: 5
Suy ra: \({x^2} = {5^2} = 25\)
b) Kết quả trên màn hình là: \(1,41421...\)
Suy ra: \({x^2} = 2\)


Ê x=6.y=7