K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
26 tháng 10 2023
Lời giải:
1.
$x^3+3x^2-16x-48=(x^3+3x^2)-(16x+48)=x^2(x+3)-16(x+3)$
$=(x+3)(x^2-16)=(x+3)(x-4)(x+4)$
2.
$4x(x-3y)+12y(3y-x)=4x(x-3y)-12y(x-3y)=(x-3y)(4x-12y)=4(x-3y)(x-3y)=4(x-3y)^2$
3.
$x^3+2x^2-2x-1=(x^3-x^2)+(3x^2-3x)+(x-1)=x^2(x-1)+3x(x-1)+(x-1)$
$=(x-1)(x^2+3x+1)$
TT
3 tháng 6 2021
a) \(2\left(x+3\right)=4x-\left(2+x\right)\)
\(2x+6=3x-2\)
\(-x=-8\)=>x=8
TT
3 tháng 6 2021
b) \(\dfrac{1}{x+2}+\dfrac{5}{2-x}=\dfrac{2x-3}{x^2-4}\) đk x khác 2 và -2
\(\dfrac{\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-3}{\left(x-2\right)\left(x+2\right)}\)
=>\(x-2-5x-10=2x-3\)
\(-6x=9=>x=\dfrac{3}{2}tm\)
12 tháng 1 2023
a:Xét ΔPBD vuông tại P và ΔMDB vuông tại M có
BD chung
góc PBD=góc MDB
Do đo: ΔPBD=ΔMDB
=>góc HBD=góc HDB
=>HB=HD
Xét tứ giác BHDK có
BH//DK
BK//DH
HB=HD
Do đó: BHDK là hình thoi
b: BHDK là hình thoi
nên HK là trung trực của BD(1)
ABCD là hình thoi
mà AC cắt BD tại O
nên O là trung điểm của BD(2), AC là trung trực của BD(3)
Từ (1), (2), (3) suy ra O,H,K,A,C thẳng hàng
TP
3
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 8 2021
\(E=\left(x^2-4x+4\right)-9=\left(x-2\right)^2-9\ge-9\)
\(E_{min}=-9\) khi \(x=2\)
3 tháng 8 2021
\(E=x^{^{ }2}-4x-5=x^2-2.2x+2^2-9=\left(x-2\right)^2-9\)
=>MIN(E)=-9
dấu '=' xảy ra <=>x-2=0=>x=2
vậy MIN (E)=-9 khi x=2
10 tháng 7 2021
\(A=\left(t+2\right)\left(3t-1\right)-t\left(3t+3\right)-2t+7\)
\(=3t^2-t+6t-2-3t^2-3t-2t+7\)
\(=\left(3t^2-3t^2\right)-\left(t-6t+3t+2t\right)-\left(2-7\right)\)
\(=0-0-\left(-5\right)=5\)
HV
10 tháng 7 2021
A=(t+2)(3t−1)−t(3t+3)−2t+7A=(t+2)(3t−1)−t(3t+3)−2t+7
=3t2−t+6t−2−3t2−3t−2t+7=3t2−t+6t−2−3t2−3t−2t+7
=(3t2−3t2)−(t−6t+3t+2t)−(2−7)=(3t2−3t2)−(t−6t+3t+2t)−(2−7)
=0−0−(−5)=5
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2022
\(x^4-8x=x\left(x^3-8\right)=x\left(x-2\right)\left(x^2+2x+4\right)\)
\(x^2-y^2-6x+9=\left(x^2-6x+9\right)-y^2=\left(x-3\right)^2-y^2=\left(x+y-3\right)\left(x-y-3\right)\)
1 tháng 12 2021
a,Ta có B = x2-x+x = x2
Mà x2 ≥ 0 với ∀ x.Dấu ''='' xảy ra <=> x=0
Vậy Min B = 0 tại x = 0
b,Ta có 4x-x2+3 = -x2+4x-4+7
= -(x2-4x+4)+7
= -(x-2)2+7
Mà (x-2)2 ≥ 0 với ∀ 0 => -(x-2)2 ≤ 0 => -(x-2)2+7 ≤ 7
Dâu ''='' xảy ra <=> -(x-2)2 = 0 <=> x-2 = 0 <=> x=2
Vậy Max c = 7 tại x = 2.
c,Ta có 2x-2x2-5 = -x2+2x-1-x2-4
= -(x-1)2-x2-4
Mà (x-1)2 ≥ 0 => -(x-1)2 ≤ 0
x2 ≥ 0 => -x2 ≤ 0
Ta có D đạt GTLN <=> -(x-1)2 = 0 hoặc -x2 = 0
-Xét -(x-1)2 = 0 <=> x = 1. Khi đó ta có D = -5
-Xét -x2 = 0 <=> x = 0. Khi đó ta có D = -5
Vậy Max D = -5 tại x = 0 hoặc x = 1
3 tháng 6 2021
a) Vì ABCD là hình bình hành ( gt )
⇒ AD // BC
F ∈ BC
⇒ AD // BF
⇒ ∠EDA = ∠EFB ( hai góc so le trong )
Xét △AED và △BEF, có :
∠EDA = ∠EFB ( cmt )
∠AED = ∠FEB ( hai góc đối đỉnh )
⇒ △AED ∼ △BEF (g-g)
b) Vì ABCD là hình bình hành ( gt )
⇒ AB // CD
E ∈ AB
⇒ BE // CD
Xét △FDC, có :
BE // CD ( cmt )
E ∈ DF ; B ∈ DC
⇒ \(\dfrac{FB}{FC}=\dfrac{EB}{DC}\) (Hệ quả của định lí Ta-let)
⇒ \(\dfrac{BF}{BE}=\dfrac{FC}{DC}\) (1)
Vì △AED ∼ △BEF ( cmt )
⇒ \(\dfrac{AE}{BE}=\dfrac{AD}{BF}\) (TSDD)
⇒ \(\dfrac{AE}{AD}=\dfrac{BE}{BF}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{AE}{AD}=\dfrac{CF}{CD}\)
⇒ AD.CD = AE.CF
c) Xét △DGC, có :
AE // DC ( cmt )
G ∈ AC ; G ∈ DE
⇒ \(\dfrac{DG}{DE}=\dfrac{GC}{AC}\) (Hệ quả của định lí Ta-let) (3)
Xét △FGC, có :
AD // CF ( cmt )
G ∈ AC ; G ∈ DF
⇒ \(\dfrac{DG}{DF}=\dfrac{AG}{AC}\) (Hệ quả của định lí Ta-let) (4)
Từ (3) và (4) ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}=\dfrac{GC}{AC}+\dfrac{AG}{AC}\)
⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}\) = 1
⇒ \(\dfrac{1}{DG}\left(\dfrac{DG}{DE}+\dfrac{DG}{DF}\right)=\dfrac{1}{DG}\)
⇒ \(\dfrac{1}{DG}=\dfrac{1}{DE}+\dfrac{1}{DF}\)
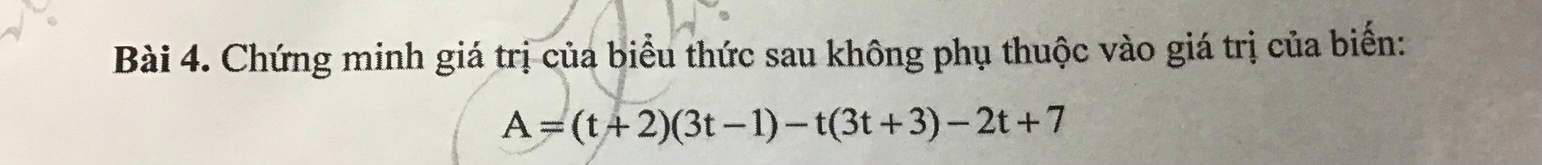
\(4x^2+4x=80\Leftrightarrow4x^2+4x-80=0\)
\(\Leftrightarrow4x^2+4x+1-81=0\Leftrightarrow\left(2x+1\right)^2-9^2=0\)
\(\Leftrightarrow\left(2x-8\right)\left(2x+10\right)=0\Leftrightarrow x=4;x=-5\)
Trả lời:
\(4x^2+4x=80\)
\(\Leftrightarrow4x^2+4x-80=0\)
\(\Leftrightarrow4x^2+4x+1-81=0\)
\(\Leftrightarrow\left(4x^2+4x+1\right)-81=0\)
\(\Leftrightarrow\left(2x+1\right)^2-81=0\)
\(\Leftrightarrow\left(2x+1-9\right)\left(2x+1+9\right)=0\)
\(\Leftrightarrow\left(2x-8\right)\left(2x+10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-8=0\\2x+10=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-5\end{cases}}}\)
Vậy x = 4; x = - 5 là nghiệm của pt.