K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 11 2017
Câu trả lời hay nhất: + ta chứng minh a,b,c có ít nhất một số chia hết cho 3
giả sử cả 3 số trên đều không chia hết cho 3
=> a^2 = 1 (mod3) và b^2 = 1 (mod3) (bình phương 1 số chia hết cho 3 hoạc chia 3 dư 1)
=> a^2 + b^2 = 2 (mod3) nhưng c^2 = 1 (mod3) => mâu thuẫn
Vậy có ít nhất 1 số chia hết cho 3
+ tương tự,có ít nhất 1 số chia hết cho 4,vì giả sử cả 3 số a,b,c đều không chia hết cho 4
=> a^2 = 1 (mod4) và b^2 = 1 (mod4) => a^2 + b^2 = 2 (mod 4) nhưng c^2 = 1 (mod 4) => mâu thuẫn
vậy có ít nhất 1 số cgia hết cho 4
+ tương tự a^2 = 1 (mod 5) hoạc a^2 = -1 (mod 5) hoạc a^2 = 4 (mod 5)
và -1 + 1 = 0,1 + 4 = 5,-1 + 4 = 3
=> phải có ít nhất 1 số chia hết cho 5
Vậy abc chia hết cho BCNN(3,4,5) = 60 hay abc chia hết 60
2 tháng 12 2017
a+5b ⋮ 7
=> 3(a+5b) ⋮7
=> 3a+15b⋮7
=> 3a+15b +7a -14b⋮7
=> 10a+b⋮7
chúc bn hok tốt ^_^
12 tháng 10 2021
a: \(B=3\left(1+3+3^2+...+3^{120}\right)⋮3\)
b: \(B=4\left(3+...+3^{119}\right)⋮4\)
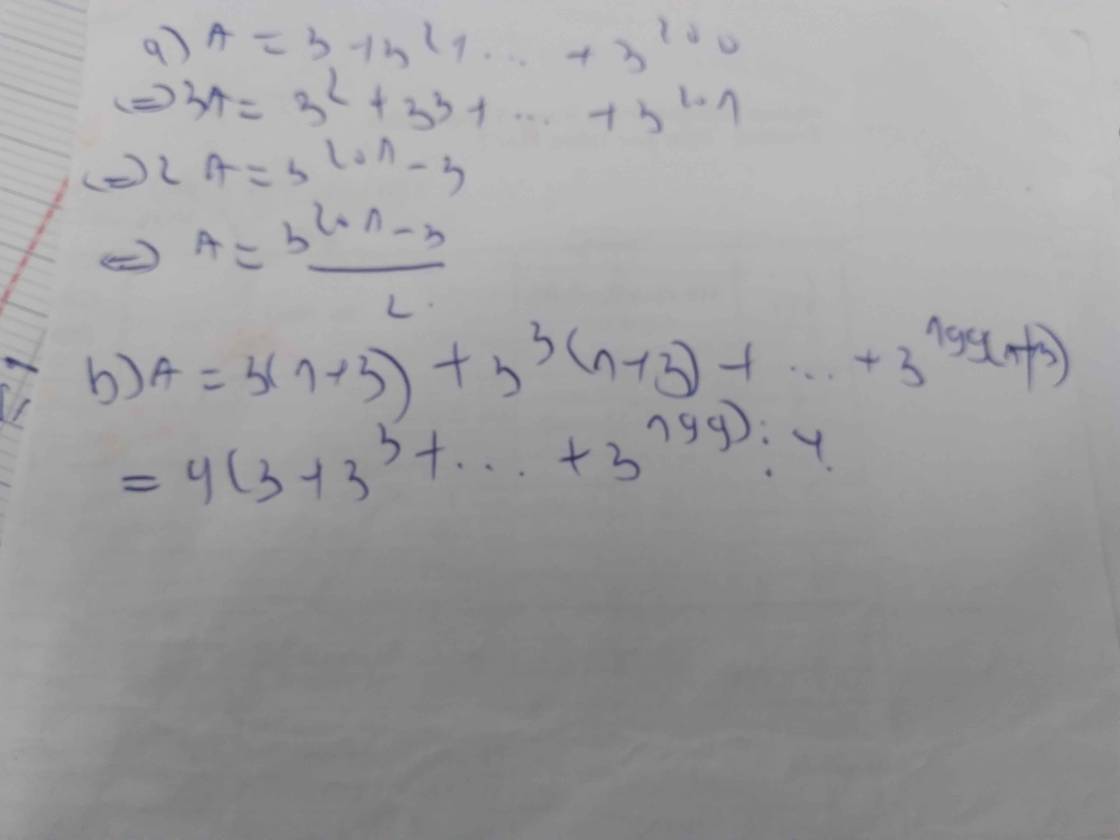
Đặt \(A=\frac{4c-13}{c-1}=\frac{\left(4c-4\right)-9}{c-1}=\frac{4\left(c-1\right)-9}{c-1}=4-\frac{9}{c-1}\)
Để 4c-13 chia hết cho c-1 thì A nguyên
=> \(\frac{9}{c-1}\inℤ\Rightarrow c-1\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
\(\Rightarrow c\in\left\{-8;-2;0;2;4;10\right\}\)
\(4c-13⋮c-1\)
\(4\left(c-1\right)-9⋮c-1\)
\(-9⋮c-1\)hay \(c-1\inƯ\left(-9\right)=\left\{\pm1;\pm3;\pm9\right\}\)