Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(y'=2cos2x=0\Rightarrow cos2x=0\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
Do \(x\in\left[0;\frac{\pi}{2}\right]\Rightarrow x=\frac{\pi}{4}\)
\(cos2x< 0\) khi \(\frac{\pi}{4}< x< \frac{\pi}{2}\); \(cos2x>0\) khi \(0< x< \frac{\pi}{4}\)
Hàm số đồng biến trên \(\left(0;\frac{\pi}{4}\right)\) nghịch biến trên \(\left(\frac{\pi}{4};\frac{\pi}{2}\right)\)
b/ \(y'=-2sin2x=0\Rightarrow sin2x=0\Rightarrow x=\frac{k\pi}{2}\)
Do \(x\in\left(-\frac{\pi}{4};\frac{\pi}{4}\right)\Rightarrow x=0\)
Hàm số đồng biến trên \(\left(-\frac{\pi}{4};0\right)\) nghịch biến trên \(\left(0;\frac{\pi}{4}\right)\)


Lê Huy Hoàng:
a) ĐK: $x\in\mathbb{R}\setminus \left\{k\pi\right\}$ với $k$ nguyên
PT $\Leftrightarrow \tan ^2x-4\tan x+5=0$
$\Leftrightarrow (\tan x-2)^2+1=0$
$\Leftrightarrow (\tan x-2)^2=-1< 0$ (vô lý)
Do đó pt vô nghiệm.
c)
ĐK:.............
PT $\Leftrightarrow 1+\frac{\sin ^2x}{\cos ^2x}-1+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+(1-\sqrt{3})\tan x-\sqrt{3}=0$
$\Rightarrow \tan x=\sqrt{3}$ hoặc $\tan x=-1$
$\Rightarrow x=\pi (k-\frac{1}{4})$ hoặc $x=\pi (k+\frac{1}{3})$ với $k$ nguyên
d)
ĐK:.......
PT $\Leftrightarrow \tan x-\frac{2}{\tan x}+1=0$
$\Leftrightarrow \tan ^2x+\tan x-2=0$
$\Leftrightarrow (\tan x-1)(\tan x+2)=0$
$\Rightarrow \tan x=1$ hoặc $\tan x=-2$
$\Rightarrow x=k\pi +\frac{\pi}{4}$ hoặc $x=k\pi +\tan ^{-2}(-2)$ với $k$ nguyên.
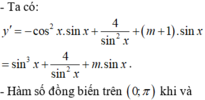
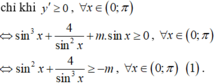
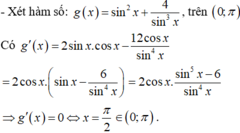
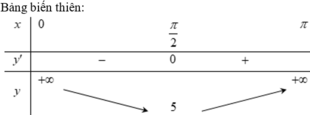
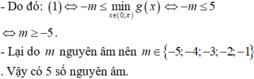
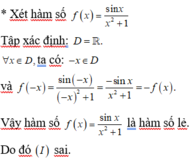
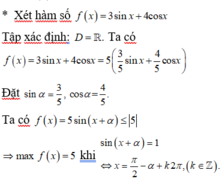

Câu 40: D
Câu 41: D
Câu 42: B
Câu 43: B