Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Do \(\overrightarrow{v}\) cùng phương với \(\overrightarrow{u}\) nên \(\overrightarrow{v}=\left(a;a\right)\) với a là số thực khác 0
Chọn \(M\left(0;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=a+0=a\\y_{M'}=a+0=a\end{matrix}\right.\) \(\Rightarrow M'\left(a;a\right)\)
Thay vào pt d' ta được:
\(a+a-4=0\Rightarrow a=2\)
\(\Rightarrow\overrightarrow{v}=\left(2;2\right)\)
\(\Rightarrow\left|\overrightarrow{v}\right|=2\sqrt{2}\)
2.
Gọi \(\overrightarrow{u}=\left(a;b\right)\)
Gọi \(A\left(0;1\right)\) là 1 điểm thuộc d
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{u}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=a\\y_{A'}=b+1\end{matrix}\right.\)
Thay tọa độ A' vào pt d' ta được: \(a+b+1-5=0\Leftrightarrow a+b=4\)
Ta có:
\(\left|\overrightarrow{u}\right|=\sqrt{a^2+b^2}\ge\sqrt{\frac{1}{2}\left(a+b\right)^2}=2\sqrt{2}\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=2\sqrt{2}\) khi \(a=b=2\)

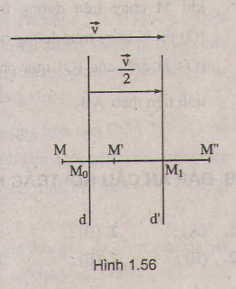
Lấy M tùy ý. Gọi (M) = M',
(M') = M''. Ta có
\(\overrightarrow{MM'}=\overrightarrow{MM'}+\overrightarrow{M'M''}=2\overrightarrow{M_oM'}+2\overrightarrow{M'M_1}=2\overrightarrow{M_oM_1}\)\(=2\dfrac{\overrightarrow{v}}{2}=\overrightarrow{v}\).
Vậy M'' = (M) =
(
(M)), với mọi M
Do đó phép tịnh tiến theo vectơ v là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d'.

Lấy điểm M bao nhiêu cũng được nhưng với điều kiện thay vào pt d phải thỏa mãn
Ví dụ bài này lấy M(0;1) thay vào d: 3.0+5.1+3=0 (sai)
Nên lấy như vậy giải kết quả cũng sẽ sai
Chắc pt d là \(3x+5y+3=0\) ?
Gọi \(\overrightarrow{v}=\left(a;b\right)\Rightarrow a^2+b^2=2\) (1)
Gọi \(M\left(-1;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=-1+a\\y_{M'}=b\end{matrix}\right.\) thay vào pt (d') ta được:
\(3\left(-1+a\right)+5b-5=0\)
\(\Leftrightarrow b=\frac{8-3a}{5}\)
Thế vào (1): \(a^2+\left(\frac{8-3a}{5}\right)^2=2\)
\(\Leftrightarrow34a^2-48a+14=0\Rightarrow\left[{}\begin{matrix}a=1\Rightarrow b=1\\a=\frac{7}{17}\Rightarrow b=\frac{23}{17}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}\overrightarrow{v}=\left(1;1\right)\\\overrightarrow{v}=\left(\frac{7}{17};\frac{23}{17}\right)\end{matrix}\right.\)

d' là ảnh của d qua phép tịnh tiến nên pt d' có dạng \(3x+4y+c=0\)
Gọi \(A\left(0;-\frac{5}{4}\right)\) là 1 điểm thuộc d, A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
Ta có \(A'\left(1;-\frac{17}{4}\right)\) mà A' thuộc d'
\(\Rightarrow3.1+4.\left(-\frac{17}{4}\right)+c=0\Rightarrow c=14\)
Phương trình d': \(3x+4y+14=0\)
\(d\left(d;d'\right)=d\left(A;d'\right)=\frac{\left|0+4\left(-\frac{17}{4}\right)+14\right|}{\sqrt{3^2+4^2}}=\frac{3}{5}\)

vì \(\overrightarrow{W}\) có giá vuông góc với đường thẳng \(d\) nên ta đặc \(\overrightarrow{W}\left(2k;-3k\right)\)
theo công thức ta có : \(\left\{{}\begin{matrix}x'=x+2k\\y'=y-3k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=x'-2k\\y=y'+3k\end{matrix}\right.\)
\(\Rightarrow2\left(x'-2k\right)-3\left(y+3k\right)+3=0\)
\(\Leftrightarrow2x'-4k-3y'-9k+3=0\Leftrightarrow2x'-3y'-13k+3\left(1\right)\)
để \(\left(1\right)\) là đường thẳng \(d\) thì : \(-13k+3=-5\Leftrightarrow k=\dfrac{8}{13}\)
\(\Rightarrow\overrightarrow{W}\left(\dfrac{16}{13};-\dfrac{24}{13}\right)\) vậy \(\overrightarrow{W}\left(\dfrac{16}{13};-\dfrac{24}{13}\right)\)

a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8

Gọi M′ ( x′ ; y′ ) ∈ d' là ảnh của M( x , y ) ∈ d qua phép tịnh tiến theo vecto ⃗v (2;3)
\(\Rightarrow\left\{{}\begin{matrix}x'=x+2\\y'=y+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=x'-2\\y=y'-3\end{matrix}\right.\)
do M (x' ; y') \(\in\) d nên
\(3x-5y+3=0\)
\(\Rightarrow3\left(x'-2\right)-5\left(y'-3\right)+3=0\)
\(\Leftrightarrow3x'-5y'+12=0\left(d'\right)\)
vậy \(M'\left(x';y'\right)\in d':3x'-5y'+12=0\)

Đặt \(\overrightarrow{v}=\left(a;b\right)\Rightarrow a^2+b^2=5\) (1)
Đường thẳng d nhận \(\left(3;-4\right)\) là 1 vtpt nên cũng nhận \(\overrightarrow{u}=\left(4;3\right)\) là 1 vtcp
\(sin\alpha=\dfrac{2}{\sqrt{5}}\Rightarrow cos\alpha=\sqrt{1-sin^2\alpha}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow\dfrac{\left|a.4+b.3\right|}{\sqrt{a^2+b^2}.\sqrt{4^2+3^2}}=\dfrac{1}{\sqrt{5}}\Leftrightarrow\left|4a+3b\right|=5\) (2)
Từ (1) và (2) ta được hệ: \(\left\{{}\begin{matrix}a^2+b^2=5\\\left|4a+3b\right|=5\end{matrix}\right.\)
Phá trị tuyệt đối, sử dụng phép thế để giải hệ ta được:
\(\left(a;b\right)=\left(-2;1\right);\left(\dfrac{2}{5};-\dfrac{11}{5}\right);\left(2;-1\right);\left(-\dfrac{2}{5};\dfrac{11}{5}\right)\)
Tổng cộng có 4 vecto \(\overrightarrow{v}\) thỏa mãn
Tới đây bạn tự làm nốt phần tìm ảnh của d nhé
Em cảm ơn thầy ạ!! ^^