K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DP
26 tháng 7 2017
a) Ta có : \(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{y}{12}\) (1)
\(\frac{x}{6}=\frac{y}{5}\Rightarrow\frac{x}{12}=\frac{y}{10}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{10}=\frac{x}{8}-\frac{2y}{24}+\frac{z}{10}=\frac{x-2y+z}{8-24+10}=\frac{27}{-6}=\frac{9}{-2}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{x}{8}=\frac{9}{-2}\Rightarrow x=-36\\\frac{y}{12}=\frac{9}{-2}\Rightarrow y=-54\\\frac{z}{10}=\frac{9}{-2}\Rightarrow z=-45\end{cases}}\)
Vậy ....
b) Ta có : \(5x=9y\Rightarrow x=\frac{9y}{5}\)
Thay \(x=\frac{9y}{5}\)vào biểu thức \(2x-3y=30\);ta được :
\(\frac{2.9y}{5}-3y=30\Rightarrow18y-15y=150\Rightarrow3y=150\Rightarrow y=50\)
Với \(y=50\Rightarrow x=\frac{9.50}{5}=90\)
Vậy .....
c) Ta có : \(x\div y\div z=3\div4\div5\)
\(\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{2x^2}{18}=\frac{2y^2}{32}=\frac{3z^2}{75}=\frac{2x^2-2y^2-3z^2}{18+32-75}=\frac{-100}{-25}=4\)
Do đó : \(\hept{\begin{cases}\frac{x}{3}=4\Rightarrow x=12\\\frac{y}{4}=4\Rightarrow y=16\\\frac{z}{5}=4\Rightarrow z=20\end{cases}}\)
Vậy ...
d) Ta có : \(2x=3y\Rightarrow x=\frac{3y}{2}\left(1\right)\)
\(5y=7z\Rightarrow z=\frac{5y}{7}\left(2\right)\)
Thay (1) và (2) vào biểu thức \(3x-7y+5z=-30\);ta được :
\(\frac{3.3y}{2}-7y+\frac{5.5y}{7}=-30\)
\(\Leftrightarrow63y-98y+50y=-420\)
\(\Leftrightarrow15y=-420\Rightarrow y=-28\)
Với \(y=-28\Rightarrow x=\frac{3.-28}{2}=-42;z=\frac{5.-28}{7}=-20\)
e) Ta có : \(3x=7y\Rightarrow\frac{x}{7}=\frac{y}{3}\)
\(\Rightarrow x.y=84\Rightarrow3k.7k=84\Rightarrow21k^2=84\Rightarrow k^2=4\Rightarrow\orbr{\begin{cases}k=2\\k=-2\end{cases}}\)
Với \(k=2\Rightarrow\frac{x}{7}=2\Rightarrow x=14;\frac{y}{3}=2\Rightarrow y=6\)
Với \(k=-2\Rightarrow\frac{x}{7}=-2\Rightarrow x=-14;\frac{y}{3}=-2\Rightarrow y=-6\)
Vậy ...
26 tháng 7 2017
a) ta có:
\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{4}=\frac{y}{6}\)
\(\Rightarrow\frac{x}{4}=\frac{y}{6}=\frac{z}{5}\)
\(\frac{y}{6}=\frac{2y}{12}\)
\(\Rightarrow\frac{x}{4}=\frac{2y}{12}=\frac{z}{5}\) (1)
áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\frac{x}{4}=\frac{2y}{12}=\frac{z}{5}=\frac{x-2y+z}{4-12+5}=\frac{27}{-3}=-9\) (2)
từ (1) và (2) suy ra:
\(\frac{x}{4}=-9\Rightarrow x=-9.4=-36\)
..................................y;z bn tự tính ha!^^
b) ta có:
\(5x=9y\Rightarrow\frac{x}{9}=\frac{y}{5}\)
\(\frac{x}{9}=\frac{2x}{18};\frac{y}{5}=\frac{3y}{15}\)
thui làm đến bước này thì bn tự làm nốt nha! làm câu d cũng tương tự lun! (câu c mk ko pik làm đâu!^^)
e)
ta có:
3x=7y \(\Rightarrow\frac{x}{7}=\frac{y}{3}\)
đặt \(\frac{x}{7}=\frac{y}{3}=k\left(k\in Z\right)\Rightarrow\hept{\begin{cases}x=7k\\y=3k\end{cases}}\)
vì xy = 84 nên : 7k.3k = \(84\)
\(\Rightarrow21k^2=84\)
\(\Rightarrow k^2=4=2^2=\left(-2\right)^2\)
với k = 2 thì x =........... ; y=................
với k=-2 thì x=........ ; y=....................
ự làm nốt ha!the end!^^
23 tháng 10 2016
1.C1 Ta có : x/2=y/5=>(x/2)^2=(y/5)^2=x/2.y/5=xy/10=40/10=4=>x=4 hoặc -4, y=10 hoặc -10
C2 : Đặt x/2=y/5=k(k khác 0) => x=2k , y=5k
Ta có xy=40=>2k5k=10k^2=40=>k^2=4=>k=-2 hoặc k=2
Với k=-2=>x=-4,y=-10
Với k=2 => x=4,y=10
Vậy
23 tháng 10 2016
Toán tỉ lệ thức dễ , đây là 4 phần gồm 4 loại khác nhau
VT
1
17 tháng 11 2021
a) xy+ 3x - 7y = 21
x.(y+3) - 7y = 21
x.(y+3) - 7y- 21 = 0
x.(y+3)- (7y+21) = 0
x.(y+3) - 7.(y+3) = 0
(y+3). (x-7) = 0
có 2 trường hợp
Nếu x-7 = 0 thì x=7 và y thuộc Z
Nếu y+3=0 thì x=-3 và x thuộc Z
NT
3
10 tháng 10 2021
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{x+2y}{7+2\cdot5}=\dfrac{51}{17}=3\)
Do đó: x=21; y=15
10 tháng 10 2021
a) \(\Rightarrow\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{2y}{10}=\dfrac{x+2y}{7+10}=\dfrac{51}{17}=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.7=21\\y=3.5=15\end{matrix}\right.\)
b) \(\dfrac{x}{5}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{25}=\dfrac{y^2}{16}=\dfrac{x^2-y^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=\dfrac{25}{9}\\y^2=\dfrac{16}{9}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\\\left\{{}\begin{matrix}x=-\dfrac{5}{3}\\y=-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
c) \(\dfrac{x}{y}=\dfrac{2}{5}\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=2k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=10k^2=40\Rightarrow k=\pm2\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=4\\y=10\end{matrix}\right.\\\left\{{}\begin{matrix}x=-4\\y=-10\end{matrix}\right.\end{matrix}\right.\)
KV
0
5 tháng 2 2022
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)
Do đó: x=-28; y=-12
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+2y}{6+2\cdot5}=\dfrac{20}{16}=\dfrac{5}{4}\)
Do đó: x=15/2; y=25/4
5 tháng 2 2022
a) \(3x = 7y \)
\(\Rightarrow \dfrac{x}{7} = \dfrac{y}{3} \)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{7} = \dfrac{y}{3}=\dfrac{x-y}{3-7}=\dfrac{-16}{-8}=2\)
Từ đây ta có :
\(\dfrac{x}{7}=2 \Rightarrow x=14\)
\(\dfrac{y}{3} = 2 \Rightarrow y = 6\)
Vậy \(x = 14 ; y = 6\)
b) Ta có : \(\dfrac{y}{5} = \dfrac{2y}{10} \)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{y}{5}=\dfrac{2y}{10}=\dfrac{x}{6} = \dfrac{x+2y}{6+10}\) \(= \dfrac{20}{16}=\dfrac{5}{4}\)
Từ đây ta có :
\(\dfrac{x}{6} = \dfrac{5}{4} \Rightarrow\dfrac{15}{2}\)
\(\dfrac{y}{5} = \dfrac{5}{4} \Rightarrow \dfrac{25}{4}\)
Vậy \(x = \dfrac{15}{2} ; y = \dfrac{25}{4}\)
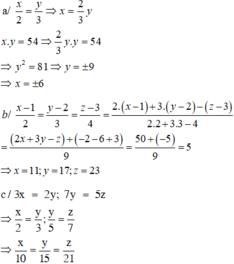
\(3x=7y\Rightarrow\frac{x}{7}=\frac{y}{3}\)
đặt \(k=\frac{x}{7}=\frac{y}{3}\Rightarrow x=7k,y=3k\)
\(\Rightarrow xy=7k.3k=21k^2=2100\Rightarrow k^2=100\Rightarrow\orbr{\begin{cases}k=10\\k=-10\end{cases}}\)
\(k=10\Rightarrow x=70,y=30\)
\(k=-10\Rightarrow x=-70,y=-30\)
Vậy x=70 và y=30, x=-70 và y=-30
\(3x=7y\)
\(\Leftrightarrow\frac{x}{7}=\frac{y}{3}\)
\(\Leftrightarrow\frac{x^2}{49}=\frac{xy}{21}=\frac{y^2}{9}\)
\(\Leftrightarrow\frac{x^2}{49}=\frac{y^2}{9}=\frac{2100}{21}=100\)
\(\Leftrightarrow\hept{\begin{cases}\frac{x^2}{49}=100\\\frac{y^2}{9}=100\end{cases}\Leftrightarrow\hept{\begin{cases}x^2=4900\\y^2=900\end{cases}}}\Leftrightarrow\hept{\begin{cases}x=\pm70\\y=\pm30\end{cases}}\)
Vậy \(\left(x,y\right)\in\left\{\left(-70,-30\right);\left(70,30\right)\right\}\)
!!!