K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 9 2021
\(3x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}\Rightarrow\dfrac{x}{15}=\dfrac{y}{9};9z=7y\Rightarrow\dfrac{z}{7}=\dfrac{y}{9}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{9}=\dfrac{z}{7}\)
Áp dụng...
\(\dfrac{x}{15}=\dfrac{y}{9}=\dfrac{z}{7}=\dfrac{3x}{45}=\dfrac{2y}{18}=\dfrac{4z}{28}=\dfrac{3x-2y-4z}{45-18-28}=\dfrac{10}{-1}=-10\\ \Rightarrow\left\{{}\begin{matrix}x=-150\\y=-90\\z=-70\end{matrix}\right.\)
23 tháng 9 2021
\(3x=5y\)
\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{3}\)
hay \(\dfrac{x}{15}=\dfrac{y}{9}\left(1\right)\)
7y=9z
nên \(\dfrac{y}{9}=\dfrac{z}{7}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{x}{15}=\dfrac{y}{9}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{15}=\dfrac{y}{9}=\dfrac{z}{4}=\dfrac{3x-2y-4z}{45-18-16}=\dfrac{10}{11}\)
Do đó: \(x=\dfrac{150}{11};y=\dfrac{90}{11};z=\dfrac{40}{11}\)
29 tháng 7 2023
P(x)+Q(x)
=3x^2y-2x+5xy^2-7y^2+3xy^2-7y^2-9x^2y-x-5
=8xy^2-14y^2-6x^2y-3x-5
=>Chọn A
NT
3
AK
18 tháng 7 2018
\(3x+2y=7y-3x\)
\(\Leftrightarrow3x+3x=7y-2y\)
\(\Leftrightarrow6x=5y\)
\(\Leftrightarrow\frac{x}{5}=\frac{y}{6}\)và \(x-y=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{5}=\frac{y}{6}=\frac{x-y}{5-6}=\frac{10}{-1}=-10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{5}=-1\\\frac{y}{6}=-1\end{cases}\Rightarrow\hept{\begin{cases}x=-1.5=-5\\y=-1.6=-6\end{cases}}}\)
Vậy \(x=-5;y=-6\)
18 tháng 7 2018
\(3x+2y=7y-3x\)
\(3x+3x=7y-2y\)
\(6x=5y\Leftrightarrow\frac{x}{5}=\frac{y}{6}\)
TTheo t/c dãy tỉ số bằng nhau
\(\Rightarrow\frac{x}{5}=\frac{y}{6}=\frac{x-y}{5-6}=\frac{10}{-1}=-10\)
\(\Rightarrow x=-50;y=-60\)
NN
3
23 tháng 9 2017
áp dụng như bài vừa nãy, nhưng biến đổi đẳng thức 3x = 2y,... thành tỉ lệ thức rùi mới làm
23 tháng 9 2017
Ta có :
\(3x=2y;7y=5z\)
\(\Rightarrow\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{7}\)
\(\Rightarrow\frac{x}{2}.\frac{1}{5}=\frac{y}{3}.\frac{1}{5};\frac{y}{5}.\frac{1}{3}=\frac{z}{7}.\frac{1}{3}\)
\(\Rightarrow\frac{x}{10}=\frac{y}{15};\frac{y}{15}=\frac{z}{21}\Leftrightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Ta lại có :
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)và x-y+z=32
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x-y+z}{10-15+21}=\frac{32}{16}=2\)
\(\Rightarrow\frac{x}{10}=2\Rightarrow x=2.10=20\)
\(\frac{y}{15}=2\Rightarrow y=15.2=30\)
\(\frac{z}{21}=2\Rightarrow z=2.21=42\)
LP
4
28 tháng 8 2019
Ta có: 6x - 2y = 7y - 3x
=> 6x + 3x = 7y + 2y
=> 9x = 9y => x = y
=> x - y = 0
mà x - y = 10 (đb)
=> ko có x; t tm
7x - 2y = 5x - 3y
=> 7x - 5x = -3y + 2y
=> 2x = -y
=> \(\frac{x}{-1}=\frac{y}{2}\) => \(\frac{2x}{-2}=\frac{3y}{6}\)
áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{-2}=\frac{3y}{6}=\frac{2x+3y}{-2+6}=\frac{20}{4}=5\)
=> \(\hept{\begin{cases}\frac{x}{-1}=5\\\frac{y}{2}=5\end{cases}}\) => \(\hept{\begin{cases}x=5.\left(-1\right)=-5\\y=5.2=10\end{cases}}\)
28 tháng 8 2019
ta có 6x-2y=7y-3x chuyển vế sang
=>9x=9y
do x-y=10 nên x=10+y
=>9(10+y)=9y
=>90+9y=9y
=>90=0y
=>y=0=>x=10
10 tháng 8 2021
5: Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
nên x=5k; y=3k
Ta có: \(x^2-y^2=4\)
\(\Leftrightarrow25k^2-9k^2=4\)
\(\Leftrightarrow k^2=\dfrac{1}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\pm\dfrac{5}{4}\\y=\pm\dfrac{3}{4}\end{matrix}\right.\)
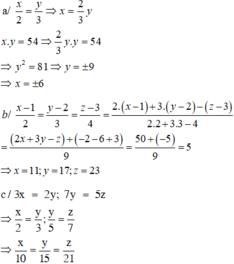
Có: \(3x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{7}=\frac{y}{3}=\frac{3x}{21}=\frac{2y}{6}=\frac{3x+2y}{21+6}=\frac{54}{27}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.7=14\\y=2.3=6\end{matrix}\right.\)
Vậy...