K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 3 2020
Ta có : 3x - 2y = 0 => 3x = 2y
=> \(\frac{3x}{6}=\frac{2y}{6}\)
=> \(\frac{x}{2}=\frac{y}{3}\)
=> \(\frac{x}{2}=\frac{3y}{9}\)
Áp dụng tính chất dãy tỉ số = nhau ta có :
\(\frac{x}{2}=\frac{3y}{9}=\frac{x+3y}{2+9}=\frac{5}{11}\)
=> \(\orbr{\begin{cases}\frac{x}{2}=\frac{5}{11}\\\frac{y}{3}=\frac{5}{11}\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{10}{11}\\y=\frac{15}{11}\end{cases}}\)
2 tháng 4 2020
Vì 3x-2y=0
=>3x=2y(1)
Vì x+3y=5
x=5-3y(2)
Thay (2) vào (1), ta có:
3(5-3y)=2y
15-9y=2y
2y+9y=15
11y=15
y=15:11
y=15/11
Thay y=15/11 vào(2), ta có:
x=5-3.15/11
x=5-45/11
x=10/11
Vậy....
Chúc bạn hok tốt,bạn nhớ k đúng cho mik nha!!!
S
23 tháng 7 2018
a, Vì \(\left|3x-2y\right|\ge0;\left|3y-4z\right|\ge0\Rightarrow\left|3x-2y\right|+\left|3y-4z\right|\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}3x-2y=0\\3y-4z=0\end{cases}\Leftrightarrow\hept{\begin{cases}3x=2y\\3y=4z\end{cases}\Leftrightarrow}\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}\\\frac{y}{4}=\frac{z}{3}\end{cases}\Leftrightarrow}\hept{\begin{cases}\frac{x}{8}=\frac{y}{12}\\\frac{y}{12}=\frac{z}{9}\end{cases}\Leftrightarrow}\frac{x}{8}=\frac{y}{12}=\frac{z}{9}}\)
\(\Leftrightarrow\frac{x}{8}=\frac{2y}{24}=\frac{3z}{27}=\frac{x-2y+3z}{8-24+27}=\frac{5}{11}\)
từ đây tìm x,y,z
b,Ta có: \(\frac{2x+3}{2}=\frac{3x-6}{5}\Rightarrow5\left(2x+3\right)=2\left(3x-6\right)\Rightarrow10x+15=6x-12\Rightarrow4x=-27\Rightarrow x=\frac{-27}{4}\)
Thay x=-27/4 vào \(\frac{3x-6}{5}=\frac{3x+3y+1}{3x}\), ta được:
\(\frac{3\cdot\left(\frac{-27}{4}\right)-6}{5}=\frac{3.\left(\frac{-27}{4}\right)+3y+1}{3.\left(\frac{-27}{4}\right)}\)
\(\Rightarrow\frac{-21}{4}=\frac{\frac{-77}{4}+3y}{\frac{-81}{4}}\Rightarrow\frac{-77}{4}+3y=\frac{1701}{16}\Rightarrow3y=\frac{2009}{16}\Rightarrow y=\frac{2009}{48}\)
Vậy x=-27/4,y=2009/48
25 tháng 6 2018
\(\hept{\begin{cases}3x=2y\\2x+y=3\end{cases}\Leftrightarrow\hept{\begin{cases}y=\frac{3}{2}.x\\2x+\frac{3}{2}.x=3\end{cases}\Leftrightarrow}\hept{\begin{cases}y=\frac{3}{2}.x\\\frac{7}{2}.x=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{6}{7}\\y=\frac{9}{7}\end{cases}}}\)
\(\hept{\begin{cases}\frac{x}{3}=\frac{3y}{4}\\3x-y=4\end{cases}\Leftrightarrow\hept{\begin{cases}4x=9y\\3x-y=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{9y}{4}\\\frac{3.9}{4}y-y=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{9}{4}.y\\\frac{23}{4}.y=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{9}{4}.y\\y=\frac{16}{23}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{36}{23}\\y=\frac{16}{23}\end{cases}}}\)
Các phần sau làm tương tự nhé
BH
24 tháng 7 2019
\(3x=2y=z\Rightarrow\frac{z}{6}=\frac{x}{2}=\frac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{z}{6}=\frac{x}{2}=\frac{y}{3}=\frac{x+y+z}{6+2+3}=\frac{99}{11}=9\)
\(\Rightarrow\hept{\begin{cases}z=54\\x=18\\y=27\end{cases}}\)
25 tháng 6 2022
a: \(3x^2\left(2x^3-x+5\right)\)
\(=3x^2\cdot2x^3-3x^2\cdot x+5\cdot3x^2\)
\(=6x^5-3x^3+15x^2\)
b: \(x^2y\left(4xy+3y-5x\right)\)
\(=x^2y\cdot4xy+x^2y\cdot3y-x^2y\cdot5x\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
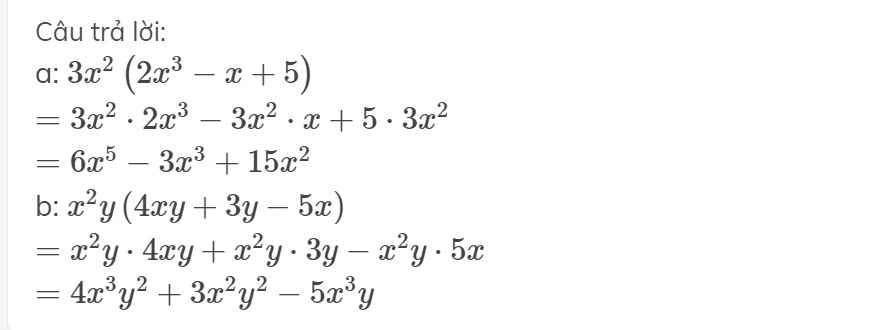
Từ \(3x-2y=0\Rightarrow3x=2y\Rightarrow\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{2}=\frac{3y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{3y}{9}=\frac{x+3y}{2+9}=\frac{5}{11}\)
\(\Rightarrow\left\{\begin{matrix}\frac{x}{2}=\frac{5}{11}\Rightarrow x=\frac{5\cdot2}{11}=\frac{10}{11}\\\frac{y}{3}=\frac{5}{11}\Rightarrow y=\frac{5\cdot3}{11}=\frac{15}{11}\end{matrix}\right.\)
Đề bài là j ?