Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo định lý Pytago ta có:
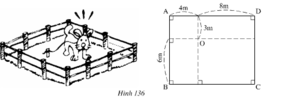
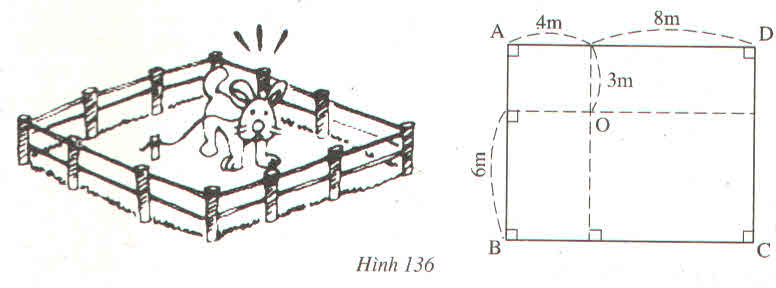
+) OA2 = 42 + 32 = 16 + 9 = 25
⇒ OA = 5m < 9m
+) OC2 = 62 + 82 = 36 + 64 = 100
⇒ OC = 10m > 9m
+) OB2 = 42 + 62 = 16 + 36 = 52
⇒ OB = √52m ≈ 7,21 (m) < 9m
+) OD2 = 32 + 82 = 9 + 64 = 73
⇒ OD = √73 ≈ 8,54(m) < 9m
Như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.
Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C
Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C
- Áp dụng định lý pi - ta - go vào \(\Delta BAD\perp A\) ta được :
\(BA^2+AD^2=BD^2\)
Thay số : \(6^2+6^2=BD^2\)
=> \(BD=6\sqrt{2}\)
Mà tứ giác ABCD là hình chữ nhật .
=> \(BD=AC=6\sqrt{2}\) ( tính chất HCN )
Vậy để con dê có thể ăn cỏ ở xa nhất thì cần 1 sợi dây dài \(6\sqrt{2}\left(m\right)\) .
khoảng tầm 8,485281374
và làm tròn là ~~ 8
tick cho mk nhé
và 
. Hơn nữa, tốc độ bơi trung bình của người đó là 1m/s và tốc độ chạy trung bình là 3m/s. Hỏi:
Chiều dài bằng \(\dfrac{4}{3}\) chiều rộng--> Chiều dài là: \(\dfrac{6.4}{3}=8\) (m)
Trong hình chữ nhật thì đường chéo dài nhất
--> Chiều dài tối thiểu của sợi dây (được tính theo py-ta-go) là:
\(\sqrt{6^2+8^2}=10\)
Vậy sợi dây cần dài tối thiểu 10m để con dê có thể ăn cỏ ở mọi nơi trong khu vườn trồng cỏ hình chữ nhật.
Áp dụng định lý Py-ta-go , ta có :
OA2 = 42 + 32 = 16 + 9 = 25
=> OA = 5
=> OA < 9
OB2 = 62 + 42 = 36 + 16 = 52
=> OB = √52
=> OB < 9
OC2 = 62 + 82 = 36 + 64 = 100
=> OC = 10
=> OC > 9
OD2 = 32 + 82 = 9 + 64 = 73
=> OD = √73
=> OD < 9
Vậy chú Cún có thể đến được các điểm A,B,D và không đến được điểm C
Bài 1 Đố: Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ vướng vào trần nhà không?
Gọi x là đường chéo của tủ. h là chiều cao của nhà. h= 21dm.
Ta có x2 = 202 + 42 = 400 + 16 = 416.
=> x = √416 (1)
Và h2 =212 = 441, => h = √441 (2)
So sánh (1) và (2) ta được x < h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.
Bài 2 : Trên giấy kẻ ô vuông ( độ dài cạnh ô vuông bằng 1 ) , cho tam giác ABC như hình 114 . Tính độ dài mỗi cạnh của tam giác ABC .
Áp dụng định lý Py-ta-go , ta có :
AB2 = 22 + 12 = 4 + 1 = 5
=> AB = √5
AC2 = 32 + 42 = 9 + 16 = 25
=> AC = 5
BC2 = 52 + 32 = 25 + 9 = 34
=> BC = √34
Vậy ...
Gửi bn bê trần ( chúc bn hc tốt )