Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức tính sai số tỉ đối
δv = =
+
=
+
= 0,014
δg = =
+
=
+2.
= 0,026
=
= 2.
= 3,95 m/s
∆v = .δv = 3,95 . 0,014 = 0,06 m/s
v = ± ∆v = 3,95 ± 0,06 m/s
mà =
=
= 9,78 m/s2.
∆g = .δg = 9,78.0,026 = 0,26 m/s2.
g = ± ∆g = 9,78 ± 0,26 m/s2

Áp dụng công thức tính sai số tỉ đối
δv = =
+
=
+
= 0,014
δg = =
+
=
+2.
= 0,026
=
= 2.
= 3,95 m/s
∆v = .δv = 3,95 . 0,014 = 0,06 m/s
v = ± ∆v = 3,95 ± 0,06 m/s
mà =
=
= 9,78 m/s2.
∆g = .δg = 9,78.0,026 = 0,26 m/s2.
g = ± ∆g = 9,78 ± 0,26 m/s2

Gọi =
vận tốc thuyền đối với bờ
=
vận tốc nước đối với bờ
=
vận tốc thuyền đối với nước
Theo định lí cộng vận tốc ta có:
=
+
=> =
-
=> =
-
=
+ (-
)
Do thuyền và nước chuyển đông ngược chiều.

v12 = v1 + v2.
Với v1 = =
= 10 km/h
và với v2 = =
= 2 km/h
=> v12 = 12 km/h.
Chọn C
Gọi =
vận tốc thuyền đối với bờ
=
vận tốc nước đối với bờ
=
vận tốc thuyền đối với nước
Theo định lí cộng vận tốc ta có:
=
+
=> =
-
=> =
-
=
+ (-
)
Do thuyền và nước chuyển đông ngược chiều.

v12 = v1 + v2.
Với v1 = =
= 10 km/h
và với v2 = =
= 2 km/h
=> v12 = 12 km/h.
Chọn C

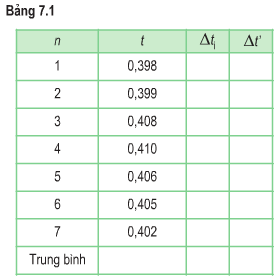
|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |


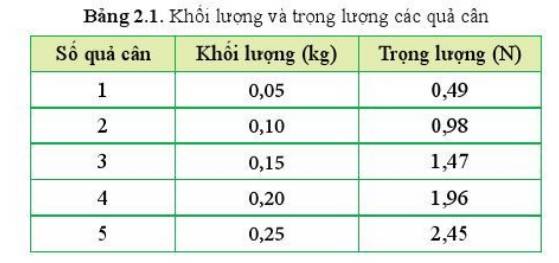
Sử dụng công thức tính trọng lực: \(P=m
.
g\)
Ta có:
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)
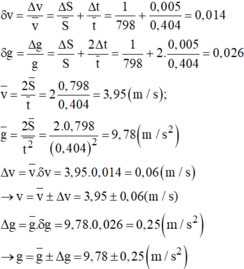
Áp dụng công thức tính sai số tỉ đối
δv = =
= 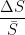 +
+ 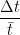 =
= 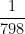 +
+ 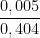 = 0,014
= 0,014
δg =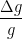 =
=  +
+ 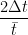 =
= 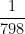 +2.
+2. 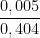 = 0,026
= 0,026
∆v =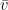 .δv = 3,95 . 0,014 = 0,06 m/s
.δv = 3,95 . 0,014 = 0,06 m/s
v =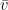 ± ∆v = 3,95 ± 0,06 m/s
± ∆v = 3,95 ± 0,06 m/s
mà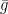 =
= 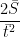 =
= 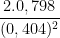 = 9,78 m/s2.
= 9,78 m/s2.
∆g =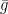 .δg = 9,78.0,026 = 0,26 m/s2.
.δg = 9,78.0,026 = 0,26 m/s2.
g =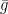 ± ∆g = 9,78 ± 0,26 m/s2
± ∆g = 9,78 ± 0,26 m/s2
Xem thêm tại: http://loigiaihay.com/bai-3-trang-44-sgk-vat-li-10-c61a7295.html#ixzz4AfIMZfly
Dương Hoàng Minh là 24h