K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 7 2018
Vì \(2x+3y=0\Rightarrow2x=-3y\Leftrightarrow\frac{x}{-3}=\frac{y}{2}\)(1)
\(4y+5z=0\Rightarrow4y=-5z\Leftrightarrow\frac{y}{-5}=\frac{z}{4}\)(2)
Từ (1) và (2)
\(\Rightarrow\frac{x}{15}=\frac{y}{-10}=\frac{z}{8}\)
Đặt \(\frac{x}{15}=\frac{y}{-10}=\frac{z}{8}=k\)
\(\Rightarrow x=15k;y=-10k;z=8k\)(3)
Thay (3) vào bt trên
\(15k.\left(-10\right)k+\left(-10\right)k.8k+15k.8k=110\)
\(\Rightarrow-150k+-80k+120k=110\)
\(\Rightarrow-110k=110\)
\(\Rightarrow k=-1\)
\(\Rightarrow x=-1.15=-15;y=-1.-10=10;z=-1.8=-8\)
15 tháng 7 2018
Ta có: \(2x+3y=0\Rightarrow2x=-3y\Rightarrow\frac{x}{-3}=\frac{y}{2}\Rightarrow\frac{x}{-15}=\frac{y}{10}\)
\(\Rightarrow\frac{x}{-15}=\frac{y}{10}=k\)
\(\Rightarrow\orbr{\begin{cases}x=-15k\\y=10k\end{cases}}\)
Ta lại có: \(4y+5z=0\Rightarrow4y=-5z\Rightarrow\frac{y}{-5}=\frac{z}{4}\Rightarrow\frac{z}{-8}=\frac{y}{10}\)
\(\Rightarrow\frac{z}{-8}=\frac{y}{10}=k\)
\(\orbr{\begin{cases}z=-8k\\y=10k\end{cases}}\)
Mà \(\text{xy + yz + xz = 110}\)
\(\Rightarrow\left(-15\right)k.10k+10k.\left(-8\right)k+\left(-15\right)k.\left(-8\right)k=110\)
\(\Rightarrow\left(-150\right)k^2+\left(-80\right)k^2+120k^2=110\)
\(\Rightarrow k^2.\left(-150+-80+120\right)=110\)
\(\Rightarrow k^2.\left(-110\right)=110\)
\(\Rightarrow k^2=110:\left(-110\right)\)
\(\Rightarrow k^2=-1\)
\(\Rightarrow k\in\varnothing\)
\(\Rightarrow x,y,z\in\varnothing\)
DH
2
19 tháng 12 2021
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{2x+3y-5z}{10+12-15}=\dfrac{2x-3y+5z}{10-12+15}\\ \Rightarrow A=\dfrac{10+12-15}{10-12+15}=\dfrac{7}{13}\)
D
22 tháng 2 2016
a, nếu x<3/2suy ra x-2<0 suy ra |x-2|=-(x-2)=2-x
(3-2x)>0 suy ra|3-2x|=3-2x
ta có: 2-x+3-2x=2x+1
5-3x=2x+1
5-1=2x+3x
6=6x nsuy ra x=6(loại vì ko thuộc khả năng xét)
nếu \(\frac{3}{2}\le x<2\)thì x-2<0 suy ra|x-2|=-(x-2)=2-x
2-2x<0 suy ra|3-2x|=-(3-2x)=2x-3
ta có:2-x+2x-3=2x+1
-1+x=2x+1
-1-1=2x-x
-2=x(loại vì ko thuộc khả năng xét)
nếu \(x\ge2\)thì x-2\(\ge\)0suy ra:|x-2|=x-2
3-2x<0 suy ra:|3-2x|=-(3-2x)=2x-3
ta có:x-2+2x-3=2x+1
3x-5=2x+1
3x-2x=5+1
x=6(chọn vì thuộc khả năng xét)
suy ra x=6
D
22 tháng 2 2016
c)\(tacó:2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{15}=\frac{y}{10}\)
\(4y=5z\Rightarrow\frac{y}{5}=\frac{z}{4}\Rightarrow\frac{y}{10}=\frac{z}{8}\)
suy ra:\(\frac{x}{15}=\frac{y}{10}=\frac{z}{8}=k\Rightarrow x=15k;y=10k;z=8k\)
ta có: 4(15k)-3(10k)+5(8k)=7
60k-30k+40k=7
70k=7 suy ra k=1/10
ta có:x=1/10.15=3/2
y=1/10.10=1
VD
1
5 tháng 4 2017
b, Ta có xy + 2x -y = 5
\(\Leftrightarrow\) x(y+2) - (y+2) = 7
\(\Leftrightarrow\) (y+ 2) (x -1) = 7
\(\Leftrightarrow\) x - 1 \(\in\) \(\left\{\pm1,\pm7\right\}\)
Lập Bảng :
| x-1 | 1 | -1 | 7 | -7 |
| x | 2 | 0 | 8 | -6 |
| y+2 | 7 | -7 | 1 | -1 |
| y | 5 | -9 | -1 | -3 |
Hơi dài nên ko giải hết đc
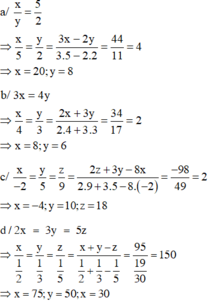
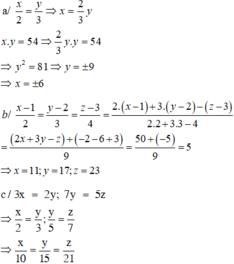
2x=3y=5z
=>\(\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\)
=>\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=k\)
=>x=15k; y=10k; z=6k
Ta có: xy=1,5
=>\(15k\cdot10k=1,5\)
=>\(150\cdot k^2=1,5\)
=>\(k^2=\dfrac{1.5}{150}=\dfrac{1}{100}\)
=>\(k=\dfrac{1}{10};k=-\dfrac{1}{10}\)
TH1: \(k=\dfrac{1}{10}\)
=>\(x=15\cdot\dfrac{1}{10}=\dfrac{15}{10}=1,5;y=\dfrac{10}{10}=1;z=\dfrac{6}{10}=0,6\)
TH2: \(k=-\dfrac{1}{10}\)
=>\(x=15\cdot\dfrac{-1}{10}=-1,5;y=\dfrac{-10}{10}=-1;z=-\dfrac{6}{10}=-0,6\)