K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 10 2020
Vào thống kê của "Wall Duong" để xem đồ thị
a) 
b) Đỉnh I\(\left(\frac{3}{4};\frac{-1}{8}\right)\)trục đối xứng d: x=\(\frac{3}{4};a=2>0\)
Cho x=0 => y=1; y=1=> x=0,x=\(\frac{1}{2}\)
c) Ta có \(y=f\left(x\right)=2x^2-3\left|x\right|+1\)là hàm số chẵn, vì f(x)=f(-x) nên đồ thị đối xứng qua trục tung
Xét x>=0 thì y=2x2-3x+1 nên đồ thị y=f(x) lấy phần của prabol (P): y=2x2-3x+1 với x>=0 sau đó lấy phần đối xứng đó qua trục tung
Số nghiệm của phương trình 2x2-3|x|+1=m là số giao điểm của đồ thị y=f(x) với đường thẳng y=m
Phương trình vô nghiệm nếu m<\(-\frac{1}{8}\), có 2 nghiệm nếu \(\orbr{\begin{cases}m=\frac{-1}{8}\\m=1\end{cases}}\), có 3 nghiệm nếu m=1, có 4 nghiệm nếu \(-\frac{1}{8}< m< 1\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
\(P=\dfrac{\left(cos^2x-sin^2x\right)^2}{4sin^2x.cos^2x}-\dfrac{1}{4sin^2x.cos^2x}=\dfrac{\left(cos^2x-1-sin^2x\right)\left(cos^2x+1-sin^2x\right)}{4sin^2x.cos^2x}\)
\(=\dfrac{-2sin^2x.2cos^2x}{4sin^2x.cos^2x}=-1\)
\(y^2-3y-1=0\) có \(ac=-1< 0\Leftrightarrow\) có 2 nghiệm trái dấu hay có 1 nghiệm dương
CM
5 tháng 5 2017
Điều kiện: x , y ≥ 1
Ta có: 2 x + y − 1 = 1 2 y + x − 1 = 1 ⇒ 2 x − 2 y + y − 1 − x − 1 = 0
⇒ 2 x − y + y − x y − 1 + x − 1 = 0 ⇒ x − y 2 − 1 y − 1 + x − 1 = 0
Khi x = y thì 2 x + x + 1 = 1 ⇒ x + 1 = 1 − 2 x (vô nghiệm do x ≥ 1 thì V T ≥ 0 , V P < 0 )
Khi y − 1 + x − 1 = 1 2 thì 2 x + 2 y + 1 2 = 2 ⇒ x + y = 3 4 (vô nghiệm vì x , y ≥ 1 )
Vậy hệ phương trình vô nghiệm
Đáp án cần chọn là: B
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
22 tháng 9 2021
1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)
24 tháng 9 2023
Tham khảo:
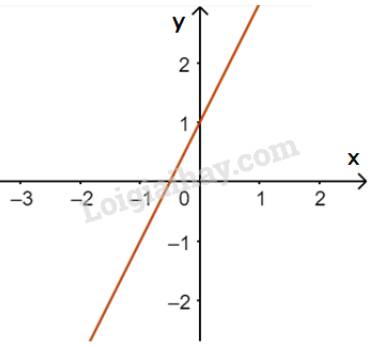
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
trình bày ra giúp mk với ạ