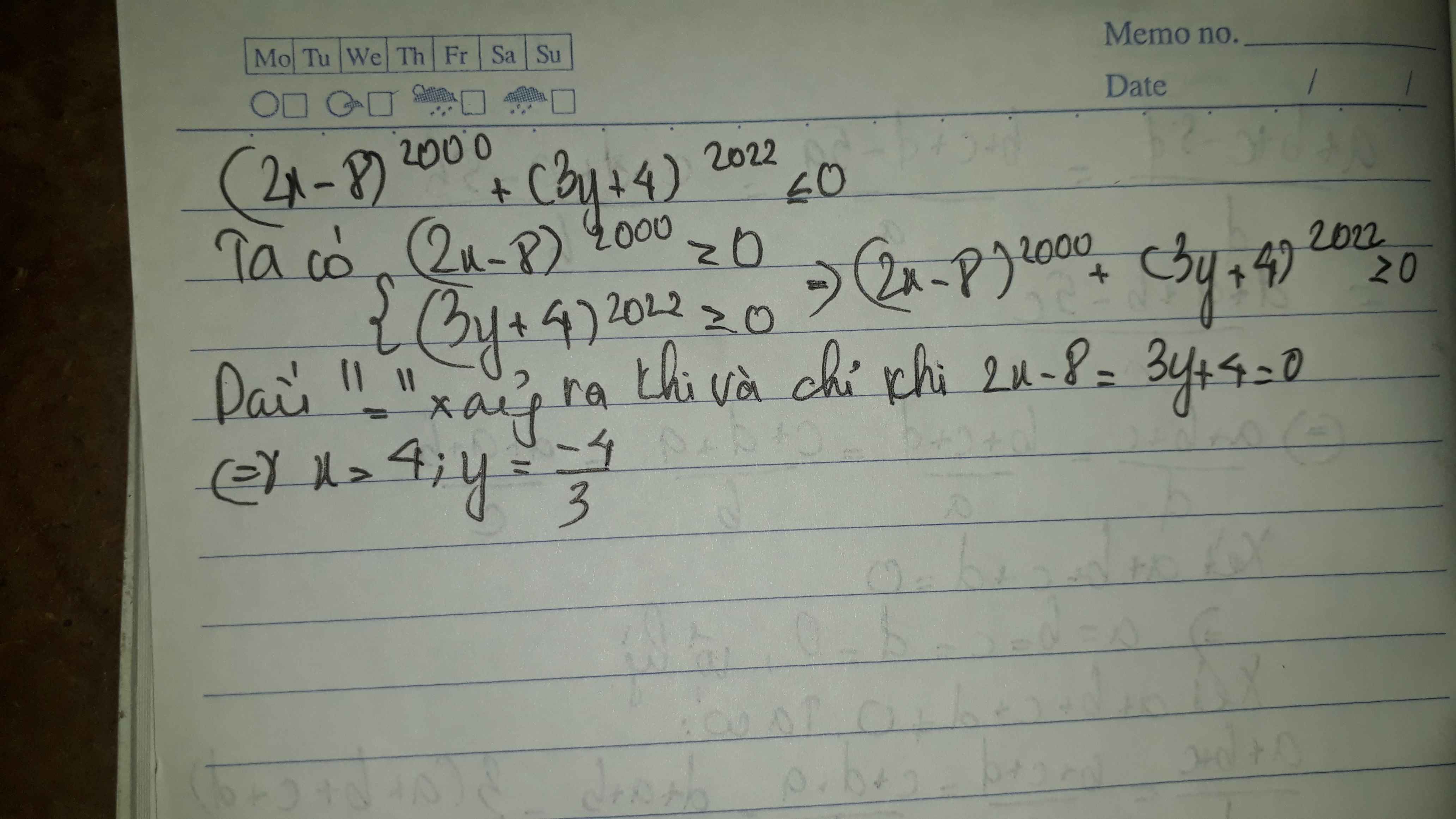N
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
0
PJ
3
KH
10 tháng 12 2015
(2x - 5)2000 + (3y + 4)2002
ta có: (2x - 5)2000 \(\ge\) 0 ; (3y + 4)2002 \(\ge\) 0
=> (2x - 5)2000 + (3y + 4)2002 \(\ge\) 0
Dấu "=" xảy ra khi 2x - 5 = 0 và 3y + 4 = 0
=> 2x = 5 và 3y = -4
=> x = 2,5 và y = \(\frac{-4}{3}\)
20 tháng 10 2017
Vì mũ của số trên là 100 và 200, đều là số chẵn
Không số nào trong số trên là số âm
Tổng là số vô âm
Tổng của chúng bằng 0
Các hiệu: (3x - 5) ; Các tổng: (2y + 1)
\(\Rightarrow3x-5=0\Rightarrow3x=5\Rightarrow x=\frac{5}{3}\)
\(\Rightarrow2y+1=0\Rightarrow2y=-1\Rightarrow y=-0,5\)
Vậy: \(x=\frac{5}{3};y=-0,5\)
N
0
3 tháng 9 2016
a) 8\(\sqrt{x}\) = \(x^2\) ( x lon hon hoac bang 0)
\(\left(8\sqrt{x}\right)^2\) = \(\left(x^2\right)^2\)
64x=\(x^4\)
\(x^4\)_ 64x = 0
x (\(x^3\) - 64) = 0
suy ra\(\orbr{\begin{cases}x=0\\x^3-64=0\end{cases}}\) suy ra \(\orbr{\begin{cases}x=0\\x^3=64\end{cases}}\) suy ran \(\orbr{\begin{cases}x=0\\x^3=4^3\end{cases}}\) suy ra \(\orbr{\begin{cases}x=0\left(tm\right)\\x=4\left(tm\right)\end{cases}}\)
Vay x= 0; x=4
b) \(\sqrt{3x-2}\) = x (x lon hon hoac bang \(\frac{2}{3}\) )
\(\left(\sqrt{3x-2}\right)^2\) = \(x^2\)
3x - 2=\(x^2\)
\(x^2-3x+2=0\)
\(^{x^2}-1x-2x+2=0\)
\(\left(x^2-1x\right)-\left(2x-2\right)=0\)
\(x\left(x-1\right)-2\left(x-1\right)=0\)
(x-1)(x-2)=0
suy ra \(\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}}\) suy ra \(\orbr{\begin{cases}x=1\left(tm\right)\\x=2\left(tm\right)\end{cases}}\)
vay \(x=1;x=2\)
27 tháng 7 2021
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
S
6 tháng 7 2019
\(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\le0\) (1)
có : \(\left(2x-5\right)^{2000}\ge0\forall x\)
\(\left(3y+4\right)^{2002}\ge0\forall x\)
\(\Rightarrow\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\ge0\) (2)
\(\left(1\right)\left(2\right)\Rightarrow\left(2x-5\right)^{2000}+\left(3y-4\right)^{2002}=0\)
\(\Rightarrow\hept{\begin{cases}\left(2x-5\right)^{2000}=0\\\left(3y+4\right)^{2002}=0\end{cases}\Rightarrow\hept{\begin{cases}2x-5=0\\3y+4=0\end{cases}\Rightarrow}\hept{\begin{cases}x=\frac{5}{2}\\y=-\frac{4}{3}\end{cases}}}\)