I
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
25 tháng 12 2018
Với tất cả các câu, mk chỉ làm ngắn gọn. Nếu bn muốn đầy đủ, thì bn tự lập bảng rồi xét.
1. \(13⋮\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
\(\Rightarrow x\in\left\{2;4;-10;16\right\}\)
Vậy x = ......................
2. \(\left(x+13\right)⋮\left(x-4\right)\)
\(\Leftrightarrow\left(x-4\right)+17⋮\left(x-4\right)\)
\(\Leftrightarrow17⋮x-4\)
\(\Leftrightarrow\left(x-4\right)\inƯ\left(17\right)=\left\{\pm1;\pm17\right\}\)
\(\Rightarrow x\in\left\{3;5;-13;21\right\}\)
Vậy x = ...................
3. \(\left(2x+108\right)⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)+105⋮\left(2x+3\right)\)
\(\Leftrightarrow105⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)\inƯ\left(105\right)\)\(=\left\{\pm1;\pm3;\pm5;\pm7;\pm15;\pm21;\pm35;\pm105\right\}\)
\(\Rightarrow x=-2;-1;-3;0;-4;1;-5;2;...............\)
4. \(17x⋮15\)
\(\Leftrightarrow x⋮15\) ( vì \(\left(15,17\right)=1\) )
Do đó : Với mọi x thuộc Z thì \(17x⋮15\)
HN
25 tháng 12 2018
6. \(\left(x+16\right)⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)+15⋮\left(x+1\right)\)
\(\Leftrightarrow15⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\inƯ\left(15\right)=\left\{\pm1;\pm3;\pm5;\pm15\right\}\)
\(\Rightarrow x\in\left\{-2;0;-4;2;-6;4;-16;14\right\}\)
Vậy x = .....................
7. \(x⋮\left(2x-1\right)\)
Mà \(\left(2x-1\right)\) lẻ
Nên : Với mọi x thuộc Z là số lẻ thì \(x⋮\left(2x-1\right)\)
8. \(\left(2x+3\right)⋮\left(x+5\right)\)
\(\Leftrightarrow\left(2x+10\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow2.\left(x+5\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow7⋮\left(x+5\right)\)
\(\Leftrightarrow\left(x+5\right)\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-12;2\right\}\)
Vậy x = .........................
10 tháng 12 2023
a: \(\left(-120\right):15+12\left(2x-1\right)=52\)
=>\(12\left(2x-1\right)-8=52\)
=>\(12\left(2x-1\right)=60\)
=>\(2x-1=\dfrac{60}{12}=5\)
=>2x=5+1=6
=>\(x=\dfrac{6}{2}=3\)
c: \(x+4⋮x+1\)
=>\(x+1+3⋮x+1\)
=>\(3⋮x+1\)
=>\(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
d: \(2x+7⋮x+2\)
=>\(2x+4+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
e: \(3x⋮x-1\)
=>\(3x-3+3⋮x-1\)
=>\(3⋮x-1\)
=>\(x-1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{2;0;4;-2\right\}\)
DH
3
28 tháng 11 2019
\(c,10⋮2x+1\)
\(\Rightarrow2x+1\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng
| 2x+1 | 1 | -1 | 2 | -2 | 5 | -5 | -10 | 10 |
| 2x | 0 | -2 | 1 | -3 | 4 | -6 | -11 | 9 |
| x | 0 | -1 | 1/2 | -3/2 | 2 | -3 | -11/2 | 9/2 |
\(d,x+13⋮x+1\)
\(x+1+12⋮x+1\)
\(\Rightarrow x+1⋮x+1\)
\(\Rightarrow12⋮x+1\)
\(\Rightarrow x+1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
Ta có bảng
| x+1 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 6 | -6 | 12 | -12 |
| x | 0 | -2 | 1 | -3 | 2 | -4 | 3 | -5 | 5 | -7 | 11 | -13 |
Bn tự KL cả 2 phần ...
28 tháng 11 2019
\(f,2x+108⋮2x+3\)
\(\Rightarrow\left(2x+3\right)+105⋮2x+3\)
\(\Rightarrow2x+3⋮2x+3\)
\(\Rightarrow105⋮2x+3\)
\(\Rightarrow2x+3\inƯ\left(105\right)=\left\{\pm1;\pm3;\pm7;\pm15;\pm21;\pm35;\pm105\right\}\)
Ta lập bảng xét
| 2x+3 | 1 | -1 | 3 | -3 | 7 | -7 | 15 | -15 | 21 | -21 | 35 | -35 | 105 | -105 |
| 2x | -2 | -4 | 0 | -6 | 4 | -10 | 12 | -18 | 18 | -24 | 32 | -38 | 102 | -108 |
| x | -1 | -2 | 0 | -3 | 2 | -5 | 6 | -9 | 9 | -12 | 16 | -19 | 51 | -54 |
Tự KL ....
6 tháng 7 2016
A) 6 chia hết cho x-1
=> x- 1 \(\in\) Ư(6) = {1 ; 2 ; 3; 6 }
thế x-1 vô từng trường hợp các ước của 6 rồi tính x
bài B ; C ; D giống như vậy
E) x +16 chia hết cho x +1
=> x+1+15 chia hết cho x +1
=> 15 chia hết cho x+1
=> x+ 1 \(\in\) Ư(15) = {1 ; 3 ; 5 ; 15}
còn lại giống bài A
Ủng hộ cho mik nha
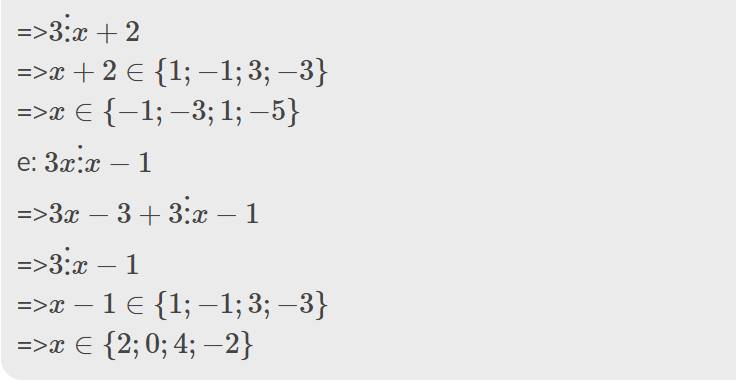
Tìm x à?
Ta có: 2x+4 chia hết cho 2x+1
2x+1+3 chia hết 2x+1
Vì 2x+1 chia hết cho 2x+1 nên 3 chia hết cho 2x+1
\(\Rightarrow\) 2x+1 \(\in\)Ư(3)=\(\left\{1;3\right\}\)
\(\Rightarrow\)x\(\in\left\{0;1\right\}\)
Ta có: x+15 chia hết cho x+1
x+1+14 chia hết cho x+1
Vì x+1 chia hết cho x+1 nên 14 chia hết cho x+1
Vậy x+1 thuộc Ư(14)
Nên x+1 \(\in\left\{1;2;7;14\right\}\)
\(\Rightarrow x\in\left\{0;1;6;13\right\}\)