K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
8 tháng 8 2016
(2x-5)2+2(2x-5)(3x+1)+(3x+1)2
=(2x-5)[(2x-5)+2(3x+1)]+(3x+1)2
=(2x-5)[8x-3]+(3x+1)2
=16x2-46x+15+9x2+6x+1
=25x2-40x+16
=(5x)2-2*5x*4+42
=(5x-4)2
PL
8 tháng 8 2016
phần nâng cao chính là một hằng đẳng thức hoàn chỉnh (a+b)2. trong đó 2x-5 là a và 3x+1 là b
M
26 tháng 10 2017
a) (x+2)(x^2-2x+4)-x(x^2+2)=15
<=> x^3 + 8 - x^3 - 2x = 15
<=> -2x = 7
<=> x = -7/2
b) (x+3)^3-x(3x+1)^2+(2x+1)(4x^2-2x+1)=28
<=> x^3 + 9x² + 27x + 27 - x(9x² + 6x + 1) + 8x^3 + 1 = 28
<=> x^3 + 9x² + 27x + 27 - 9x^3 - 6x² - x + 8x^3 + 1 - 28 = 0
<=> 3x² + 26x = 0
<=> x(3x + 26) = 0
Vậy x = 0 và x = -26/3
c) (x^2-1)^3-(x^4+x^2+1)(x^2-1)=0
<=> (x² - 1)[(x² -1)² - x^4 - x² - 1] = 0
<=> (x-1)(x+1)(x^4 - 2x² + 1 - x^4 - x² - 1 ) = 0
<=> -(x-1)(x+1)3x² = 0
Vậy nghiệm là x = 1 ; -1 ; 0
21 tháng 8 2021
`a)`
`A=(x+1)(2x-1)`
`=2x^{2}+x-1`
`=2(x^{2}+(1)/(2)x-(1)/(2))`
`=2(x^{2}+(1)/(2)x+(1)/(16)-(9)/(16))`
`=2(x+(1)/(4))^{2}-(9)/(8)>= -9/8` với mọi `x`
Dấu `=` xảy ra khi :
`x+(1)/(4)=0<=>x=-1/4`
Vậy `min=-9/8<=>x=-1/4`
``
`b)`
`(4x+1)(2x-5)`
`=8x^{2}-18x-5`
`=8(x^{2}-(9)/(4)x-(5)/(8))`
`=8(x^{2}-(9)/(4)x+(81)/(64)-(121)/(64))`
`=8(x-(9)/(8))^{2}-(121)/(8)>= -(121)/(8)` với mọi `x`
Dấu `=` xảy ra khi :
`x-(9)/(8)=0<=>x=9/8`
Vậy `min=-121/8<=>x=9/8`
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
\(A=2x^2+x-1=2\left(x+\dfrac{1}{4}\right)^2-\dfrac{9}{8}\ge-\dfrac{9}{8}\)
\(A_{min}=-\dfrac{9}{8}\) khi \(x=-\dfrac{1}{4}\)
\(B=8x^2-18x-5=8\left(x-\dfrac{9}{8}\right)^2-\dfrac{121}{8}\ge-\dfrac{121}{8}\)
\(B_{min}=-\dfrac{121}{8}\) khi \(x=\dfrac{9}{8}\)
H
18 tháng 4 2023
\(\dfrac{2x-6}{x+1}\ge0\)
`<=> 2x-6 >= 0`
`<=> 2x >=6`
`<=> x>=3`
Vật bpt đã cho có tập nghiệm \(S=\left\{x|x\ge3\right\}\)
NN
2
2
28 tháng 1 2023
`a)(2x-1)^2-0,25=0`
`<=>(2x-1-0,5)(2x-1+0,5)=0`
`<=>(2x-1,5)(2x-0,5)=0`
`<=>[(x=0,75)(x=0,25):}`
`b)x^2+9=6x`
`<=>(x-3)^2=0`
`<=>x-3=0`
`<=>x=3`
`c)(x^2-4)-3x-6=0`
`<=>(x-2)(x+2)-3(x+2)=0`
`<=>(x+2)(x-2-3)=0`
`<=>(x+2)(x-5)=0`
`<=>[(x=-2),(x=5):}`
28 tháng 1 2023
a: =>(2x-1-0,5)(2x-1+0,5)=0
=>(2x-1,5)(2x-0,5)=0
=>x=0,25 hoặc x=0,75
b: =>x^2-6x+9=0
=>(x-3)^2=0
=>x-3=0
=>x=3
c: =>(x-2)(x+2)-3(x+2)=0
=>(x+2)(x-5)=0
=>x=5 hoặc x=-2
10 tháng 12 2021
a: \(\Leftrightarrow\left(2x+5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)
29 tháng 10 2021
\(=\dfrac{x^3+x^2+x^2+x+x+1}{x^2+x}\)
\(=x+1+\dfrac{1}{x}\)
19 tháng 3 2020
=[x(x-2)/2(x2+4)-2x2/(4+x2)(2-x)][x(x-2)(x+1)/x3]
={[x(x-2)(2-x)-4x2 ]/2(2-x)(4+x2)} .[x(x-2)(x+1)/x3 ]
=[-x(x2+4)/2(2-x)(4+x2)].[x(x-2)(x+1)/x3 ]
=-x.x(x-2)(x+1)/2(2-x)x3
=(x+1)/2x
VD
2
HP
9 tháng 12 2021
\(\left(2x^3+x^2+10x+30\right):\left(2x+1\right)\)
\(=2x^3:\left(2x+1\right)+x^2:\left(2x+1\right)+10x:\left(2x+1\right)+30:\left(2x+1\right)\)
\(=2x^3:2x+2x^3:1+x^2:2x+x^2:1+10x:2x+10x:1+30:2x+30:1\)
\(=x^2+2x^3+\dfrac{1}{2}x+x^2+5+10x+15x+30\)
\(=2x^3+2x^2+\dfrac{51}{2}x+35\)
PX
1
16 tháng 7 2023
Phân tích đa thức:
x^4 + 2x^3 - x^2 - 2x + 1
= (x^4 + 2x^3) - (x^2 + 2x) + 1
= x^3(x + 2) - x(x + 2) + 1
= (x^3 - x)(x + 2) + 1
= x(x^2 - 1)(x + 2) + 1
= x(x - 1)(x + 1)(x + 2) + 1
Vậy phương trình đã cho có các nghiệm là x = -2, x = -1, x = 0 và x = 1.
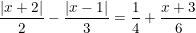
Lời giải:
Đặt $2x-1=a$
\(a^6=a^8\\ \Leftrightarrow a^8-a^6=0\\ \Leftrightarrow a^6(a^2-1)=0\\ \Leftrightarrow a^6=0\text{ hoặc } a^2-1=0\\ \Leftrightarrow a=0 \text{ hoặc } a=\pm 1\\ \Leftrightarrow 2x-1=0 \text{ hoặc } 2x-1=1 \text{ hoặc } 2x-1=-1\)
$\Leftrightarrow x=\frac{1}{2}$ hoặc $x=1$ hoặc $x=0$
Nhận xét: Mũ chẵn và chung cơ số
⇒ Cơ số ϵ { -1; 1; 0}
Ta lập bảng:
⇒ x ϵ {0; 1}