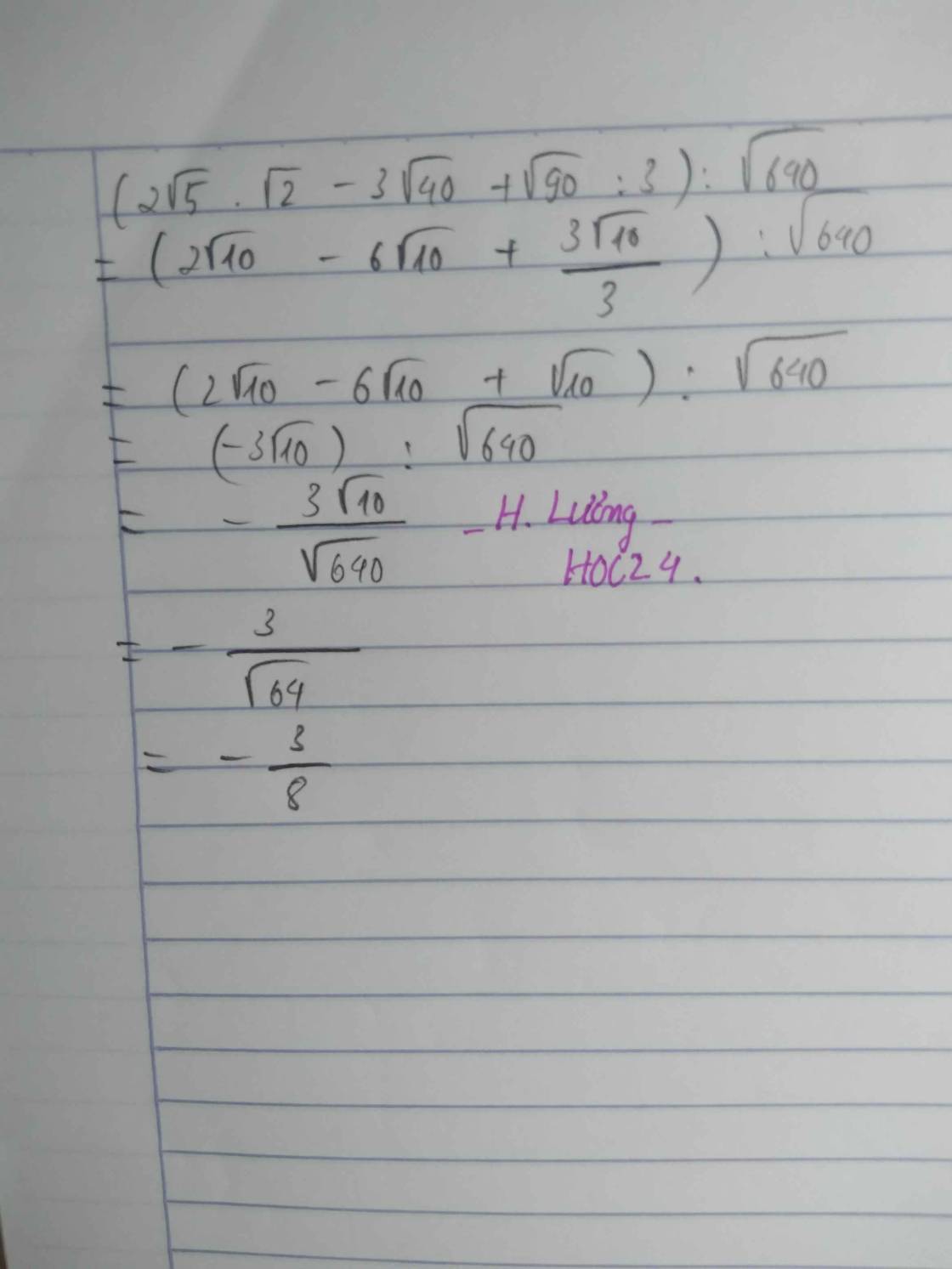\((2\sqrt5 . \sqrt2 - 3 \sqrt{40} + \sqrt{90} :3) :\sqrt{640}\)

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

MS

mini star

28 tháng 10 2023

\((2\sqrt5 . \sqrt2 - 3 \sqrt{40} + \sqrt{90} :3) :\sqrt{640}\)

1

GT

Giáp Thị Hiền Lương

28 tháng 10 2023

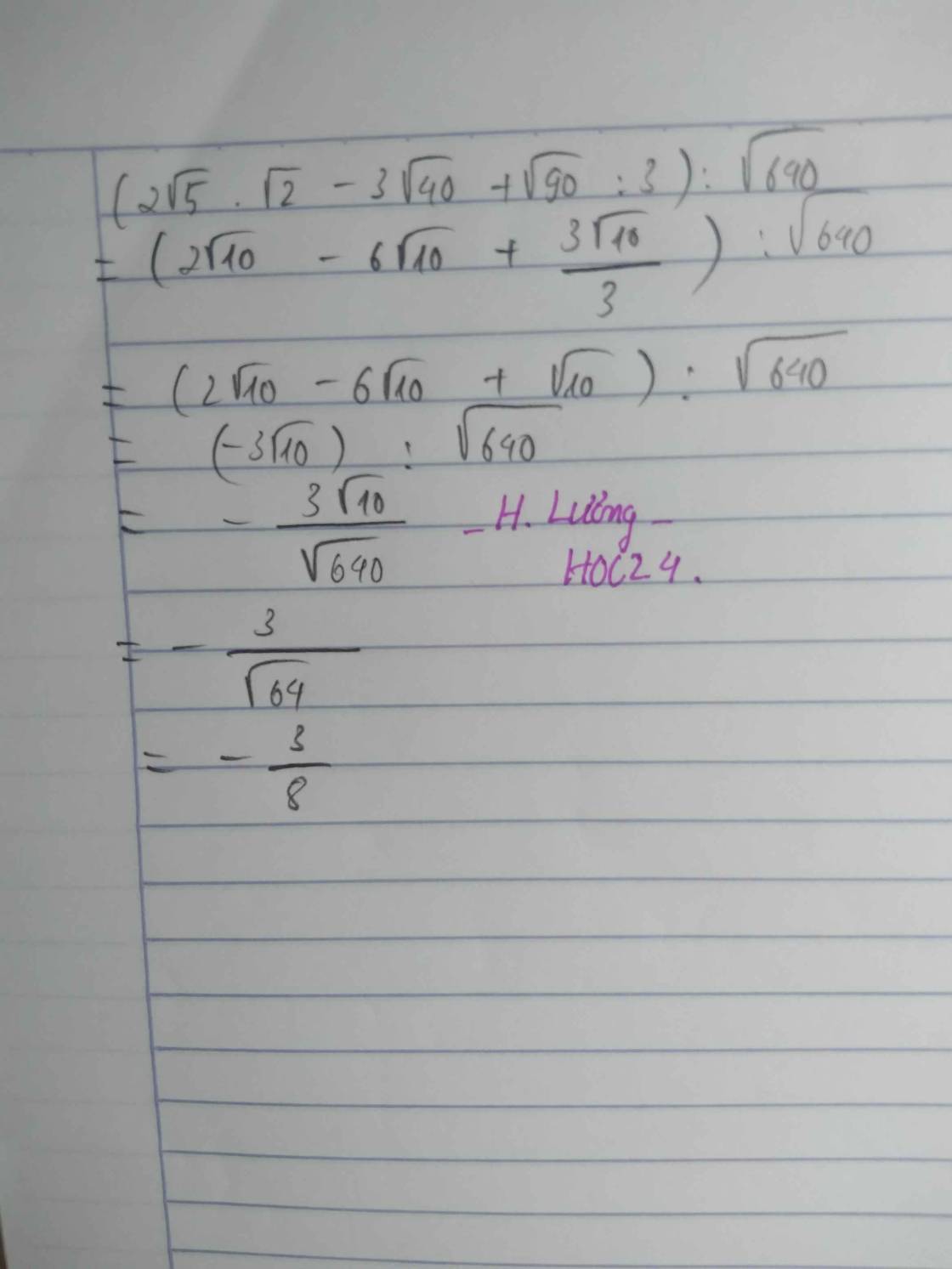loading... Chúc Bạn Học Tốt.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TH

Trần Hoàng Thiên Bảo

2 tháng 10 2016 - olm

thực hiện phép tính

\(\left(2\sqrt{5}.\sqrt{2}-3\sqrt{40}+\sqrt{90}:3\right):\sqrt{640}\)

0

NP

Ngan pham

2 tháng 10 2016 - olm

thực hiện phép tính

\(\left(2\sqrt{5}.\sqrt{2}-3\sqrt{40}+\sqrt{90}:3\right):\sqrt{640}\)

1

HL

Hoàng Lê Bảo Ngọc

2 tháng 10 2016

\(\left(2\sqrt{5}.\sqrt{2}-3\sqrt{40}+\sqrt{90}:3\right):\sqrt{640}=\left(2\sqrt{10}-6\sqrt{10}+\sqrt{10}\right):\left(8\sqrt{10}\right)\)

\(=-\frac{3\sqrt{10}}{8\sqrt{10}}=-\frac{3}{8}\)

OL

Oanh Lê

5 tháng 8 2020

1, Rút gọn A=\( \sqrt{8+2\sqrt15}\)+\(\sqrt{8-2\sqrt15} \)-2\(\sqrt{6-2\sqrt5}\) B=\(\sqrt{6+2\sqrt5-\sqrt13+\sqrt48}\) 2, Chứng minh (\(\dfrac{3\sqrt2}{\sqrt27-3}\)-\(\dfrac{\sqrt150}{3}\))*\(\dfrac{1}{\sqrt6}\)=\(\frac{-4}{3}\) Giúp mik vs. Mai mik phải nộp...

2

NT

Nguyễn Thanh Hằng

5 tháng 8 2020

1/ \(A=\sqrt{8-2\sqrt{15}}=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}=\left|\sqrt{5}-\sqrt{3}\right|=\sqrt{5}-\sqrt{3}\) (Vì \(\sqrt{5}-\sqrt{3}>0\))

\(B=\sqrt{6+2\sqrt{5}}-\sqrt{13}+\sqrt{48}=\sqrt{\left(\sqrt{5}+1\right)^2}-\sqrt{13}+4\sqrt{3}=\left|\sqrt{5}+1\right|-\sqrt{13}+4\sqrt{3}=\sqrt{5}+1+\sqrt{13}+4\sqrt{5}\)

2/Ta có :

\(\left(\frac{3\sqrt{2}}{\sqrt{27}-3}-\frac{\sqrt{150}}{3}\right).\frac{1}{\sqrt{6}}\)

\(=\left(\frac{3\sqrt{2}}{3\sqrt{3}-3}-\frac{5\sqrt{6}}{3}\right).\frac{1}{\sqrt{6}}\)

\(=\left(\frac{3\sqrt{2}}{3\left(\sqrt{3}-1\right)}-\frac{5\sqrt{6}\left(\sqrt{3}-1\right)}{3\left(\sqrt{3}-1\right)}\right).\frac{1}{\sqrt{6}}\)

\(=\frac{3\sqrt{2}-15\sqrt{2}+5\sqrt{6}}{3\left(\sqrt{3}-1\right)}.\frac{1}{\sqrt{6}}\)

\(=\frac{-12\sqrt{2}+5\sqrt{6}}{3\left(\sqrt{3}-1\right)}.\frac{1}{\sqrt{6}}\)

\(=\frac{-7+\sqrt{3}}{6}\)

Vậy...

NL

Nguyễn Lê Phước Thịnh

5 tháng 8 2020

Bài 1:

Ta có: \(A=\sqrt{8+2\sqrt{15}}+\sqrt{8-2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\)

\(=\sqrt{5+2\cdot\sqrt{5}\cdot\sqrt{3}+3}+\sqrt{5-2\cdot\sqrt{5}\cdot\sqrt{3}+3}-2\cdot\sqrt{5-2\cdot\sqrt{5}\cdot1+1}\)

\(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-2\cdot\sqrt{\left(\sqrt{5}-1\right)^2}\)

\(=\left|\sqrt{5}+\sqrt{3}\right|+\left|\sqrt{5}-\sqrt{3}\right|-2\cdot\left|\sqrt{5}-1\right|\)

\(=\sqrt{5}+\sqrt{3}+\sqrt{5}-\sqrt{3}-2\cdot\left(\sqrt{5}-1\right)\)

\(=2\sqrt{5}-2\sqrt{5}+2\)

=2

Vậy: A=2

Bài 2: Sửa đề: Chứng minh \(\left(\frac{3\sqrt{2}}{\sqrt{27}-3}-\frac{\sqrt{150}}{3}\right)\cdot\frac{1}{\sqrt{6}}=\frac{-7+\sqrt{3}}{6}\)

Ta có: \(\left(\frac{3\sqrt{2}}{\sqrt{27}-3}-\frac{\sqrt{150}}{3}\right)\cdot\frac{1}{\sqrt{6}}\)

\(=\left(\frac{9\sqrt{2}}{3\left(\sqrt{27}-3\right)}-\frac{\sqrt{150}\left(\sqrt{27}-3\right)}{3\cdot\left(\sqrt{27}-3\right)}\right)\cdot\frac{1}{\sqrt{6}}\)

\(=\frac{9\sqrt{2}-45\sqrt{2}+3\sqrt{150}}{9\left(\sqrt{3}-1\right)}\cdot\frac{1}{\sqrt{6}}\)

\(=\frac{-36\sqrt{2}+3\sqrt{150}}{9\sqrt{6}\cdot\left(\sqrt{3}-1\right)}\)

\(=\frac{\sqrt{54}\cdot\left(5-4\sqrt{3}\right)}{\sqrt{486}\cdot\left(\sqrt{3}-1\right)}\)

\(=\frac{5-4\sqrt{3}}{3\sqrt{3}-3}\)

\(=\frac{-7+\sqrt{3}}{6}\)(đpcm)

MS

mini star

29 tháng 10 2023

\(\sqrt{(\sqrt3 - \sqrt5 )^2} - \sqrt{(1-\sqrt5)^2} +\dfrac{ 3 }{\sqrt3}\)

1

H9

HT.Phong (9A5)

CTVHS

29 tháng 10 2023

\(\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}-\sqrt{\left(1-\sqrt{5}\right)^2}+\dfrac{3}{\sqrt{3}}\)

\(=\left|\sqrt{3}-\sqrt{5}\right|-\left|1-\sqrt{5}\right|+\dfrac{\left(\sqrt{3}\right)^2}{\sqrt{3}}\)

\(=\left(\sqrt{5}-\sqrt{3}\right)-\left(\sqrt{5}-1\right)+\sqrt{3}\)

\(=\sqrt{5}-\sqrt{3}-\sqrt{5}+1+\sqrt{3}\)

\(=1\)

ST

Sơn Thanh

29 tháng 6 2018 - olm

1/ Rút gọn các biểu thức sau :

a. \(\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}} \)

b.\(\sqrt{3-\sqrt5}- \sqrt{3+\sqrt5}\)

1

KT

Không Tên

30 tháng 6 2018

a) \(A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\)

\(\Rightarrow\)\(\sqrt{2}A=\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}\)

\(=\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{\left(\sqrt{3}+1\right)^2}\)

\(=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)

\(\Rightarrow\)\(A=\frac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}\)

b) bn lm tương tự

ST

Sơn Thanh

29 tháng 6 2018

Rút gọn các biểu thức sau :

1/ \(\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}} \)

2/ \(\sqrt{3-\sqrt5}- \sqrt{3+\sqrt5}\)

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 7 2022

1: \(=\dfrac{\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}\)

2: \(=\dfrac{\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}=-\sqrt{2}\)

TN

Thu Nguyen

25 tháng 6 2018

Rút gọn biểu thức\(\sqrt (\sqrt3-1)^2 - \sqrt(\sqrt3+1)^2 +3\sqrt2\) B) \(\sqrt(9-4\sqrt5) +\sqrt(\sqrt5+1)^2\) C) \(\sqrt25 +\sqrt49-2\sqrt16\) D) \(x^2 - 5 : x+\sqrt5 \)( chia dưới dạng phân số nha mấy bạn tại mình bấm k được) E) \(x-4+\sqrt(16-8x +x^2)\) Làm giúp mình nha mình cần gấp lắm làm rõ từng bước giúp mình nha mình sẽ chọn...

1

AT

Aki Tsuki

25 tháng 6 2018

Hỏi đáp Toán

TN

Thu Nguyen

25 tháng 6 2018

Cảm ơn bạn nha

NH

Người hâm mộ Bùi Tiến Dũng

6 tháng 11 2019

\(\sqrt{9-4\sqrt5}\) -3+ \(\sqrt2\)

Giải giúp mình câu rút gọn biểu thức này với!!

2

VH

Võ Hồng Phúc

6 tháng 11 2019

\(=\sqrt{\left(\sqrt{5}-2\right)^2}-3+\sqrt{2}\)

\(=\sqrt{5}-2-3+\sqrt{2}=\sqrt{5}+\sqrt{2}-5\)

KD

Kẹo dẻo

6 tháng 11 2019

\(\sqrt{9-4\sqrt{5}}-3+\sqrt{2}\\ =\sqrt{\left(\sqrt{5}\right)^2-2.2.\sqrt{5}+2^2}-3+\sqrt{2}\\ =\sqrt{\left(\sqrt{5}-2\right)^2}-3+\sqrt{2}\\ =\sqrt{5}-2-3+\sqrt{2}\\ =\sqrt{5}-\sqrt{2}-5\)

OL

Oanh Lê

13 tháng 8 2020

Rút gọn biểu thức:

A=\(\dfrac{4+\sqrt 2 -\sqrt 3 -\sqrt 6 +\sqrt 8}{2+\sqrt 2 -\sqrt 3}\)

B= 21(\(\sqrt{2+\sqrt3} +\sqrt{3-\sqrt5}\))\(^2\) - 6(\(\sqrt{2-\sqrt3}+ \sqrt{3+\sqrt5}\))\(^2\) - 15\(\sqrt{15}\)

Giúp em với ạ

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 8 2020

Ta có: \(B=21\left(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}}\right)^2-6\left(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}}\right)^2-15\sqrt{15}\)

\(=21\cdot\left[2+\sqrt{3}+3-\sqrt{5}+2\sqrt{\left(2+\sqrt{3}\right)\left(3-\sqrt{5}\right)}\right]-6\cdot\left[2-\sqrt{3}+3+\sqrt{5}+2\cdot\sqrt{\left(2-\sqrt{3}\right)\left(3+\sqrt{5}\right)}\right]-15\sqrt{15}\)

\(=21\cdot\left(5+\sqrt{3}-\sqrt{5}+\sqrt{\left(4+2\sqrt{3}\right)\left(6-2\sqrt{5}\right)}\right)-6\cdot\left[5-\sqrt{3}+\sqrt{5}+\sqrt{\left(4-2\sqrt{3}\right)\left(6+2\sqrt{5}\right)}\right]-15\sqrt{15}\)

\(=21\cdot\left[5+\sqrt{3}-\sqrt{5}+\left(\sqrt{3}+1\right)\left(\sqrt{5}-1\right)\right]-6\cdot\left[5-\sqrt{3}+\sqrt{5}+\left(\sqrt{3}-1\right)\left(\sqrt{5}+1\right)\right]-15\sqrt{15}\)

\(=21\cdot\left(5+\sqrt{3}-\sqrt{5}+\sqrt{15}-\sqrt{3}+\sqrt{5}-1\right)-6\cdot\left(5-\sqrt{3}+\sqrt{5}+\sqrt{15}+\sqrt{3}-\sqrt{5}-1\right)-15\sqrt{15}\)

\(=21\cdot\left(4+\sqrt{15}\right)-6\left(4+\sqrt{15}\right)-15\sqrt{15}\)

\(=84+21\sqrt{15}-24-6\sqrt{15}-15\sqrt{15}\)

\(=60\)

OL

Oanh Lê

13 tháng 8 2020

Giúp e câu a nữa ạ