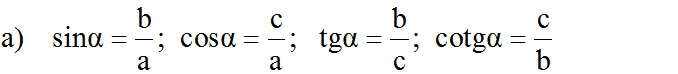Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)

Vẽ tam giác ABC vuông tại A, góc C = 34°

Theo định nghĩa ta có:

Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
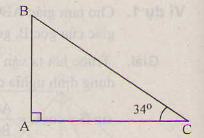
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.

Đã xảy ra lỗi rồi. Bạn thông cảm vì sai sót này.
Ta có:
Áp dụng hệ quả của bất đẳng thức Cauchy cho ba số không âm
trong đó với , ta có:
Tương tự, ta có:
Cộng ba bất đẳng thức và , ta được:
Khi đó, ta chỉ cần chứng minh
Thật vậy, bất đẳng thức cần chứng minh được quy về dạng sau: (bất đẳng thức Cauchy cho ba số )
Hay
Mà đã được chứng minh ở câu nên luôn đúng với mọi
Dấu xảy ra
Vậy,

Hướng dẫn giải:
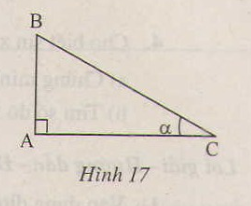
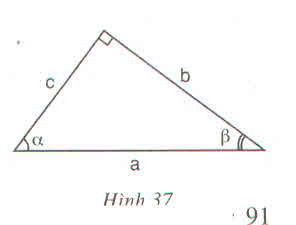
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
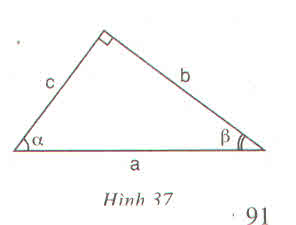
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.