Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mấy bài toán khó như thế này mik mang lên H.vn nhé
a) góc NOQ = MOP = 60oo ( vì đối đỉnh với góc MOP)
góc NOP = 180oo −60o−60o = 120oo ( vì kề bù với góc MOP)
góc MOQ = NOP = 120oo ( vì đối đỉnh với góc NOP)
b) Vì Ot' là tia đối của Ot mà tia Ot là tia phân giác của MOP và nó cũng tạo thành góc bẹt nên Ot' là tia phân giác của góc NOQ

O t x y m n k z
Bài làm
a) Vì xy cắt mn tại O
=> \(\widehat{xOn}=\widehat{mOy}\)( Hai góc đối đỉnh )
Ta có: Ot là tia phân giác của \(\widehat{xOn}\)
Mà Ok là tia đối của Ot
Do đó: Ok là tia phân giác của \(\widehat{mOy}\)( đpcm )
b) Sai đề nên tự làm lấy
# Học tốt #
#)Giải :
x y m n O t k z z'
a) Vì Ot là tia phân giác của góc \(\widehat{xOn}\)
\(\Rightarrow\widehat{xOt}=\widehat{tOn}\left(1\right)\)
\(\Rightarrow\widehat{xOn}=\widehat{kOy}\left(2\right)\) (hai góc đối đỉnh)
\(\Rightarrow\widehat{tOn}=\widehat{mOk}\left(3\right)\) (hai góc đối đỉnh)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) \(\Rightarrow\) Ok là tia phân giác của góc \(\widehat{mOy}\)
b) Kẻ thêm tia Oz' là tia phân giác của góc \(\widehat{yOn}\)
\(\Rightarrow\widehat{yOz'}=\widehat{z'On}\left(1\right)\)
C/m tương tự ý a) với hai góc đối đỉnh
Từ đó suy ra đpcm

a) Vì Ot là phân giác xOy'
=> xOt = y'Ot = 90/2 = 45 độ( xOy' = 90 độ)
Vì Ot' là phân giác x'Oy
=> yOt' = x'Ot' = 90/2 = 45 độ(x'Oy = 90 độ)
Mà t'Ot = yOt' + yOx + xOt
=> t'Ot = 90 + 45 + 45 = 180 độ
=> t'Ot là góc bẹt
=> Ot' là tia đối của Ot (dpcm)
Ý b) là OM là phân giác góc xOy và ON là pg x'Oy' à

a,b:
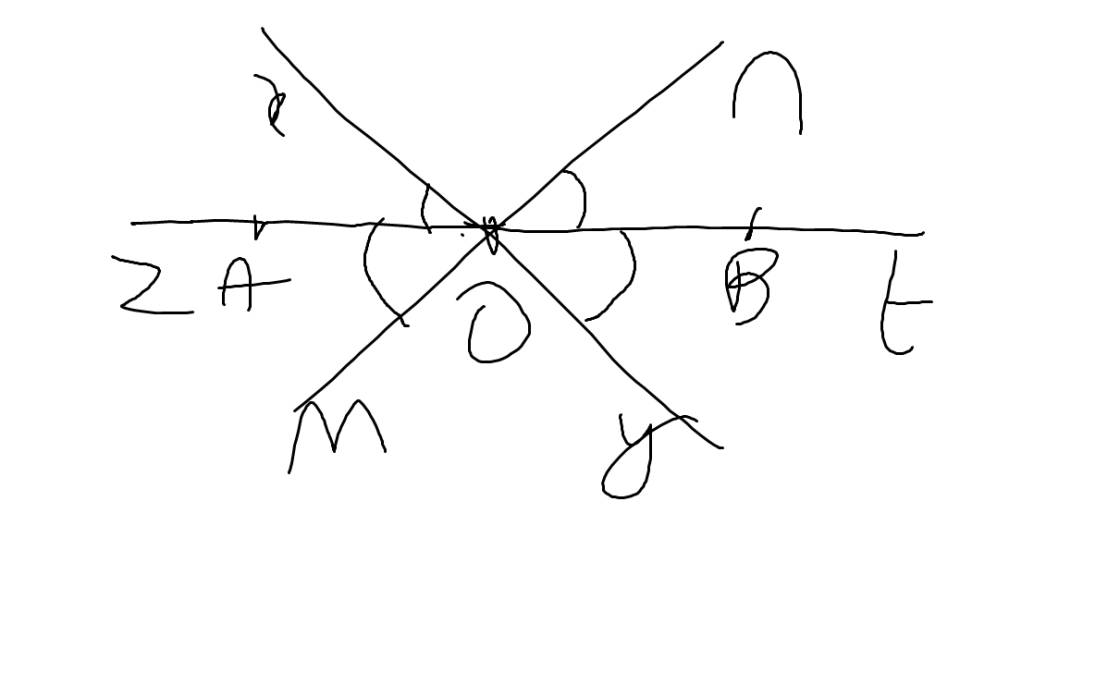
c: Ta có: \(\widehat{xOm}=\widehat{yOn}\)(hai góc đối đỉnh)
\(\widehat{xOz}=\widehat{mOz}=\dfrac{\widehat{xOm}}{2}\)(Oz là phân giác của góc xOm)
\(\widehat{tOn}=\widehat{tOy}=\dfrac{\widehat{nOy}}{2}\)(Ot là phân giác của góc nOy)
Do đó: \(\widehat{xOz}=\widehat{mOz}=\widehat{tOn}=\widehat{tOy}\)
=>\(\widehat{xOz}=\widehat{tOy}\)
mà \(\widehat{xOz}+\widehat{zOy}=180^0\)(hai góc kề bù)
nên \(\widehat{tOy}+\widehat{zOy}=180^0\)
=>\(\widehat{tOz}=180^0\)
=>\(\widehat{AOB}=180^0\)
=>A,O,B thẳng hàng

trên nửa mặt phẳng bờ chưa tia Oy có góc yOm < góc yOt ( ao < 75o ) nên tia Om nằm giữa hai tia Oy và Ot.
Suy ra góc mOt = 75o - ao
Hai góc xOm và yOm kề bù nên góc xOm = 1800 - ao
Vì tia On là tia phân giác của góc xOm nên \(\widehat{xOn}=\widehat{nOm}=\frac{180^o-a^o}{2}=90^o-\frac{a^o}{2}\)
Hai góc xOn và yOn kề bù nên
\(\widehat{yOn}=180^o-\widehat{xOn}=180^o-\left(90^o-\frac{a^o}{2}\right)=90^o+\frac{a^o}{2}\)
Trên nửa mặt phẳng bờ chưa tia Oy có \(\widehat{yOm}< \widehat{yOt}< \widehat{yOn}\) \(\left(a^o< 75^o< 90^o+\frac{a^o}{2}\right)\) nên tia Ot nằm giữa hai tia Om và On.
Để tia Ot là tia phân giác của góc mOn thì phải có thêm điều kiện
\(\widehat{mOt}=\frac{1}{2}\widehat{mOn}\Leftrightarrow75^o-a^o=\frac{1}{2}\left(90^o-\frac{a^o}{2}\right)\)
\(\Rightarrow a^o=40^o\)
x O y m n t
Ta có :
\(\widehat{xOy}=180^0\)
\(\widehat{yOt}=125^0\)
\(\Rightarrow\widehat{xOt}=55^0\)
\(\Leftrightarrow\widehat{xOt}=\widehat{tOm}=55^0\Rightarrow\widehat{xOm}=110^0\)
Ta có :
\(\widehat{yOt}=125^0\)
\(\widehat{tOm}=55^0\)
\(\Rightarrow\widehat{yOm}=125-55=70^0\)
Vậy \(\left\{{}\begin{matrix}\widehat{xOm}=110^0\\\widehat{yOm}=70^0\end{matrix}\right.\)