Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực tác dụng lên vật được biểu diễn như hình vẽ:
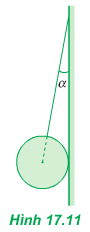
a) + Khi vật m cân bằng. Ta có:
+
=
+
=
=>
=
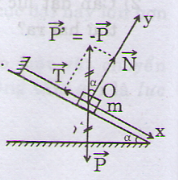
Xét \(\Delta\)P'NO, ta có: sinα = = \(\dfrac{T}{P}\)
=> T = P sin\(\alpha\)
=> T = mg sin30o = 2.9,8. \(\dfrac{1}{2}\) = 9,8 (N)
b) Ta có: cosα = = \(\dfrac{N}{P}\)
=> N = Pcosα = mgcosα = 3. 9,8.
=> N = 16,97N

216: treo ngọn đèn này vào một đầu dây
=>Độ lớn của lực căng dây là T=m*g=9,8N>8N
=>Dây sẽ bị đứt
=>Chọn B
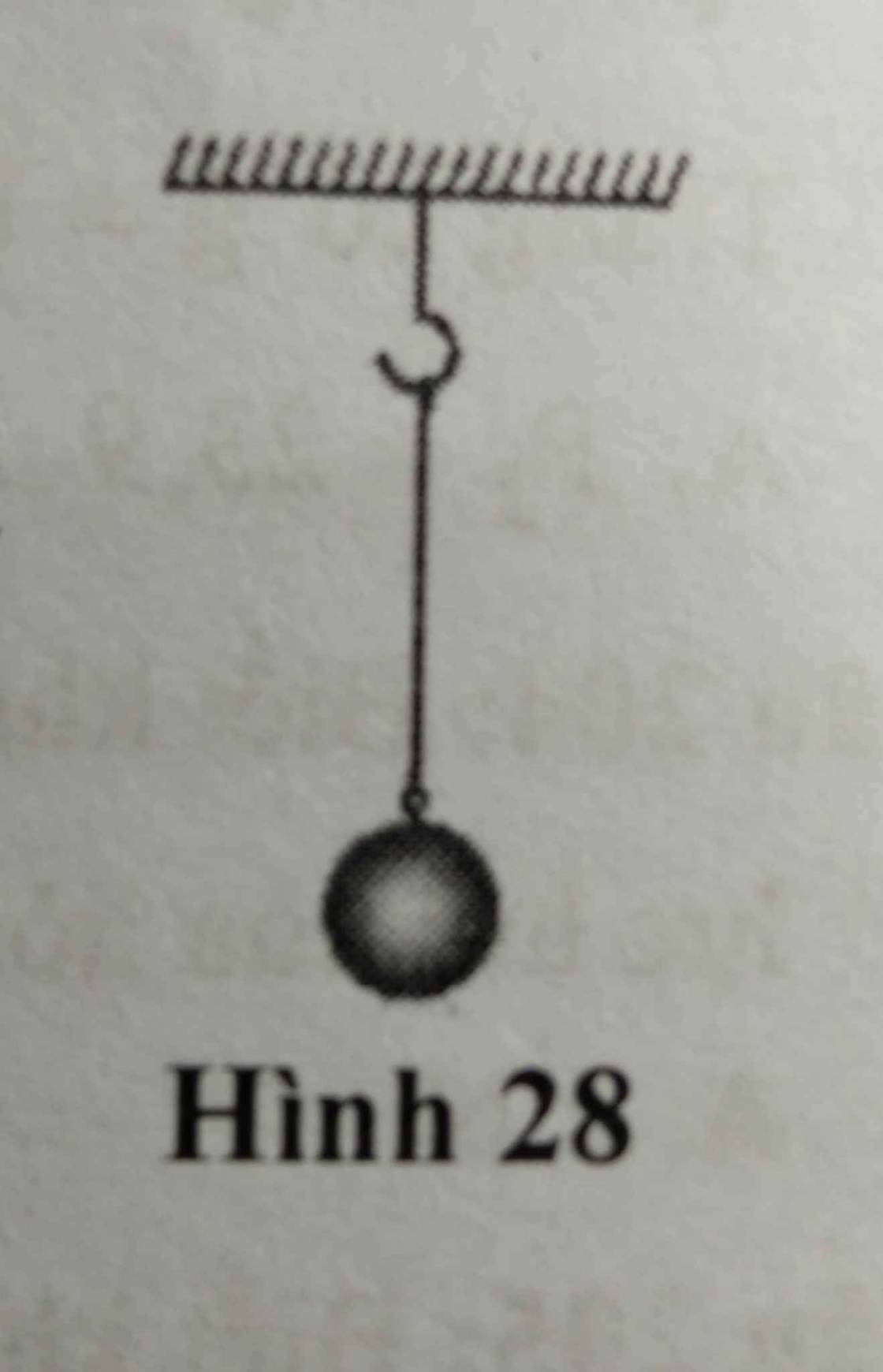
215: Bạn cho hình 28 đi bạn

$a.$ Các lực tác dụng lên bóng đèn: Trọng lực, Lực căng dây
Trọng lượng của bóng đèn là:
$P = m.g = 2.10 = 20 (N)$
Để trạng thái cân bằng, Trọng lực tác dụng lên vật phải cân bằng với lực căng dây. Do đó, độ lớn của lực căng dây là $T = 20N$
$b.$ Các lực tác dụng lên dây: Lực kéo của bóng đèn, lực giữ từ mặt tường
Lực kéo của bóng đèn với lực căng dây là cặp lực trực đối, nên lực kéo của bóng đèn có độ lớn $F = 20 N$
Dây cũng ở trạng thái cân bằng, nên lực giữ từ mặt tường có độ lớn $F' = 20N$.

có thể biểu diễn các lực trên hình ảnh giúp mình được không ạ? Được thì cảm ơn nhiều nhaaa!![]()

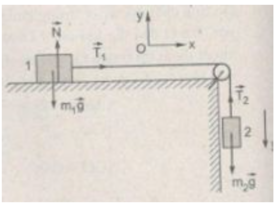
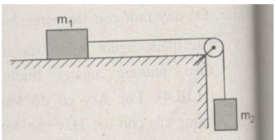
Chọn chiều dương là chiều chuyển động của dây (H.III.8G)
Từ (2) và (3)
T = m 2 (g – a) = 1,0(9,8 – 2,45) = 7,35 N

Chọn trục quay đi qua đầu B (quy ước chiều dương cùng chiều với đồng hồ quay)
Vì hệ đang cân bằng nên ta có: \(\sum M=0\)
\(\Leftrightarrow F.AB-P_m.CB=0\)
\(\Leftrightarrow10.100-10m.20=0\)
\(\Leftrightarrow m=5\left(kg\right)\)
Áp dụng định luật II Newton vào thanh AB có:
\(\overrightarrow{F}+\overrightarrow{P_m}+\overrightarrow{T_B}=\overrightarrow{0}\)
\(\Rightarrow F-10m+T_B=0\)
\(\Leftrightarrow T_B=10.5-10=40\left(N\right)\)
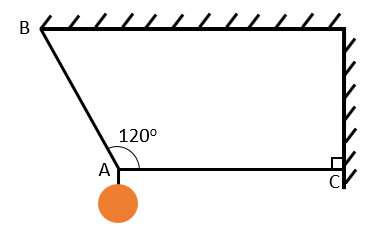
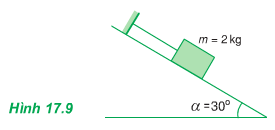

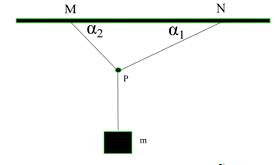
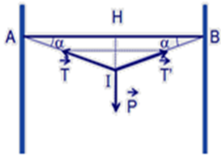

Trọng lượng của vật là: \(P=mg=9,8.8=78,4\left(N\right)\)
Áp dụng định luật II Newton ta có: \(\overrightarrow{P}+\overrightarrow{T_{AB}}+\overrightarrow{T_{AC}}=\overrightarrow{0}\) (*)
Chọn trục xOy trùng với phương của trọng lực và lực căng AC, chiều dương từ trên xuống, từ trái qua phải.
Chiếu (*) lên trục xOy ta thu được:
\(\left\{{}\begin{matrix}Ox:T_{AC}=T_{AB}sin30^0\left(1\right)\\Oy:P=T_{AB}cos30^0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Rightarrow T_{AB}\approx90,53\left(N\right)\) \(\Rightarrow T_{AC}\approx45,26\left(N\right)\)