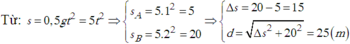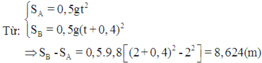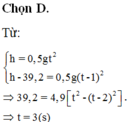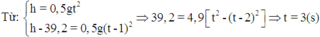Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

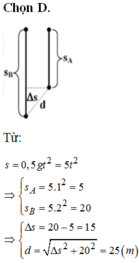
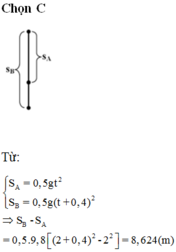
Chọn thời điểm viên bi A bắt đầu rơi làm mốc thời gian. Nếu gọi t là thời gian rơi của viên bi A thì thời gian rơi của viên bi B sẽ là t' = t + 0,5. Như vậy quãng đường mà viên bi A và B đã đi được tính theo các công thức :
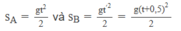
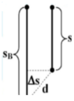
Từ đó suy ra khoảng cách giữa hai viên bi sau khoảng thời gian 2 s kể từ khi bi A bắt đầu rơi
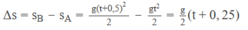
Suy ra ∆ s ≈ 11m

Nếu gọi s là quãng đường viên đá đi được sau khoảng thời gian t kể từ khi bắt đầu rơi tới khi chạm đất và gọi s 1 là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian t 1 = t -1 thì ta có các công thức
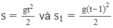
Từ đó suy ra quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:
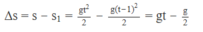
Với ∆ s = 24,5 m và g = 10 m/ s 2 , ta tìm được khoảng thời gian rơi tự do của viên đá
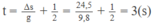

Hướng dẫn giải:
a) \(S=\frac{1}{2}gt^2\)
\(\rightarrow t=\sqrt{\frac{2S}{g}}=2s\)
b) \(v=gt=20\) m/s
Quãng đường vật rơi trong 5s đầu tiên là
S3=1/2.10.52 =125
Quãng đường vật rơi đc trong thời gian t là
S1=1/2.10.t (1)
Quảng đường vật rơi đc trong 2s cuối là
S2=1/2.10.(t-2)2
=> s1-s2=s3
-> t =7.25s thay t vào pt (2) ta đc
S=137.8125m
Còn vận tốc thì áp dụng ct tính ra thôi :))))))