Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
Đặt f(x) = \(\sqrt{x}-\sqrt{x-1}\) tập xác định [1;+∞)
Dễ thấy f(x) > 0
f(x) = \(\left(\sqrt{x}-1\right)-\sqrt{x-1}+1=\dfrac{x-1}{\sqrt{x}+1}-\sqrt{x-1}+1\)
= \(\sqrt{x-1}\left(\dfrac{\sqrt{x-1}}{\sqrt{x+1}}-1\right)+1\le\sqrt{x-1}\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)+1=\dfrac{-\sqrt{x-1}}{\sqrt{x+1}}+1\le1\)
Và f(1) = 1
Vậy f(x) có tập giá trị là (0;1]
* Nếu m \(\ge1\) thì bpt vô nghiệm
* Nếu m < 1 thì bpt có nghiệm
Vậy tập hợp m thỏa mãn là (0;1)
(0;1)
ei ~ atr ăn cắp ảnh nka , chưa xin phép eg , atr lấy ảnh eg từ khi nào vậy , khai mau

1. \(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=5\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=9\end{matrix}\right.\) ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2y+xy^2+x+y=5xy\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^4y^2+x^2y^4+x^2+y^2=25x^2y^2\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\)\(\Leftrightarrow0=16x^2y^2\)
\(\Rightarrow\) phương trình vô nghiệm

a: \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{2}{x}-\dfrac{8}{y}=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y}=11\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\\dfrac{1}{x}=-3+\dfrac{4}{y}=-3+4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{12}{x-3}-\dfrac{5}{y+2}=63\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{36}{x-3}-\dfrac{15}{y+2}=189\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{44}{x-3}=176\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=\dfrac{1}{4}\\\dfrac{15}{y+2}=-13-\dfrac{8}{x-3}=-13-32=-45\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{13}{4}\\y=-\dfrac{1}{3}-2=-\dfrac{7}{3}\end{matrix}\right.\)

Câu 1:
\(\Leftrightarrow\left\{{}\begin{matrix}13x>\dfrac{7}{3}\\4x-16< 3x-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{7}{39}\\x< 2\end{matrix}\right.\Leftrightarrow\dfrac{7}{39}< x< 2\)
mà x nguyên
nên x=1
Câu 2:
\(\Leftrightarrow\left\{{}\begin{matrix}2x< 4\\mx>2-m\end{matrix}\right.\)
=>x<2 và mx>2-m
Nếu m=0 thì bất phươg trình vô nghiệm
Nếu m<>0 thì BPT sẽ tương đương với:
\(\left\{{}\begin{matrix}x< 2\\x>\dfrac{2-m}{m}\end{matrix}\right.\)
Để BPT vô nghiệm thì 2-m/m>=2
=>\(\dfrac{2-m}{m}-2>=0\)
=>\(\dfrac{2-m-2m}{m}>=0\)
=>\(\dfrac{3m-2}{m}< =0\)
=>0<m<=2/3

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
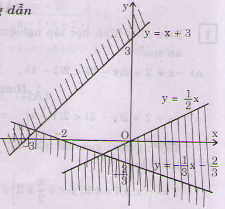
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
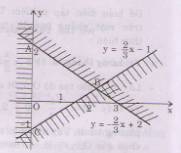

a)\(\left\{{}\begin{matrix}2x-3y=1\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(3-2y\right)-3y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6-7y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=3-2\cdot\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=\dfrac{11}{7}\end{matrix}\right.\)b) Biểu diễn lại một biến theo một biến như pt trên rồi giải, ta có :
\(\left\{{}\begin{matrix}2x+4y=5\\4x-2y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{10}\\y=\dfrac{4}{5}\end{matrix}\right.\)
c) Cách làm tương tự như pt a ta có :
\(\left\{{}\begin{matrix}\dfrac{2}{3}x+\dfrac{1}{2}y=\dfrac{2}{3}\\\dfrac{1}{3}x-\dfrac{3}{4}y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{8}\\y=-\dfrac{1}{6}\end{matrix}\right.\)
d) Tương tự ta có :
\(\left\{{}\begin{matrix}0,3x-0,2y=0,5\\0,5x+0,4y=1,2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(1.\left(x\ne\pm1\right)\Rightarrow pt\Leftrightarrow\left(x-m\right)\left(x-1\right)=\left(x+1\right)\left(x-2\right)\)
\(\Leftrightarrow x^2-x\left(m+1\right)+m=x^2-x-2\)
\(\Leftrightarrow-x\left(m+1\right)+m=-x-2\)
\(\Leftrightarrow x=\dfrac{m+2}{m}\left(m\ne0\right)\)
\(pt-có-ngo-duy-nhất\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m+2}{m}\ne1\\\dfrac{m+2}{m}\ne-1\end{matrix}\right.\)\(\Leftrightarrow m\ne-1\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-1\end{matrix}\right.\)
\(2.\left\{{}\begin{matrix}x^2+8y^2=12\left(1\right)\\x^3+2xy^2+12y=0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow x^3+2xy^2+y\left(x^2+8y^2\right)=0\)
\(\Leftrightarrow\left(x+2y\right)\left(x^2-xy+4y^2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2y\left(3\right)\\x^2-xy+4y^2=\left(x-\dfrac{y}{2}\right)^2+\dfrac{15}{4}y^2=0\left(4\right)\end{matrix}\right.\)
\(\left(3\right)\left(1\right)\Rightarrow4y^2+8y^2=12\Leftrightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-2\\y=-1\Rightarrow x=2\end{matrix}\right.\)
với \(x=y=0\) không là nghiệm của hệ pt
với \(x=y\ne0\Rightarrow\left(4\right)>0\Rightarrow\left(4\right)-vô-nghiệm\)
\(\Rightarrow\left(x;y\right)=\left\{\left(-2;1\right);\left(2;-1\right)\right\}\)
\(1,\Leftrightarrow\left(x-m\right)\left(x-1\right)=x^2-x-2\\ \Leftrightarrow x^2-x-mx+m-x^2+x+2=0\\ \Leftrightarrow mx=m+2\)
PT có nghiệm duy nhất \(\Leftrightarrow m\ne0\)
\(2,\Leftrightarrow\left\{{}\begin{matrix}x^2y+8y^3=12y\\x^3+2xy^2+12y=0\end{matrix}\right.\)
Thế \(PT\left(1\right)\rightarrow PT\left(2\right)\Leftrightarrow x^3+2xy^2+x^2y+8y^3=0\)
\(\Leftrightarrow\left(x+2y\right)\left(x^2-2xy+4y^2\right)+xy\left(x+2y\right)=0\\ \Leftrightarrow\left(x+2y\right)\left(x^2-xy+4y^2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-2y\\\left(x-\dfrac{1}{2}y\right)^2+\dfrac{15}{4}y^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2y\\\left\{{}\begin{matrix}x-\dfrac{1}{2}y=0\\y^2=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2y\\x=y=0\end{matrix}\right.\)
Thay \(x=y=0\Leftrightarrow0+0=12\left(loại\right)\)
Thay \(x=-2y\Leftrightarrow4y^2+8y^2=12y^2=12\Leftrightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-2\\y=-1\Rightarrow x=2\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(-2;1\right);\left(2;-1\right)\right\}\)