Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: TH1: Chọn 1 điểm trong 2 điểm M,N; 1 điểm trong 3 điểm P,Q,R
Số cách chọn 1 điểm trong 2 điểm M,N là 2 cách
Số cách chọn 1 điểm trong 3 điểm P,Q,R là 3 cách
=>Có 2*3=6(cách)
TH2: Vẽ đường thẳng PQR
=>Có 1 cách
TH3: Vẽ đường thẳng MN
=>Có 1 cách
Tổng số đường thẳng là:
6+1+1=8(đường)
b: TH1: Chọn 1 điểm trong 5 điểm thẳng hàng, chọn 1 điểm trong 4 điểm không thẳng hàng
Số cách chọn 1 điểm trong 5 điểm thẳng hàng là 5 cách
Số cách chọn 1 điểm trong 4 điểm không thẳng hàng là 4 cách
=>Có 5*4=20 đường thẳng
TH2: Vẽ 1 đường thẳng đi qua 5 điểm thẳng hàng
=>Có 1 đường thẳng
TH3: Chọn 2 điểm trong 4 điểm không thẳng hàng
=>Có \(C^2_4=6\left(đường\right)\)
Số đường thẳng tất cả là:
20+1+6=27(đường)

Cứ mỗi 1 cặp thì vẽ được 1 đường thẳng
=>9 điểm thì được 4 cặp và 1 điểm
vì đề bảo các cặp => 4x1=4(đường thẳng)

KO có 3 điểm nào thẳng hàng => số đường thảng = số điềm là n số đường thẳng là K
=> \(K=\frac{n.\left(n-1\right)}{2}\) mà K = 28 => n.(n-1) = 56 => n =7 =>số điểm là 7
gọi số điểm cho trước là n ( n>1)
Theo bài ra ta có : n(n-1):2=28
n(n-1)=56
n(n-1)=7.8
vì n(n-1)là 2 stn liên tiếp , 56 viết dc tích 2 stn liên tiếp là: 8 và 9
vậy số điểm cần tìm là 9 "_" :)))))

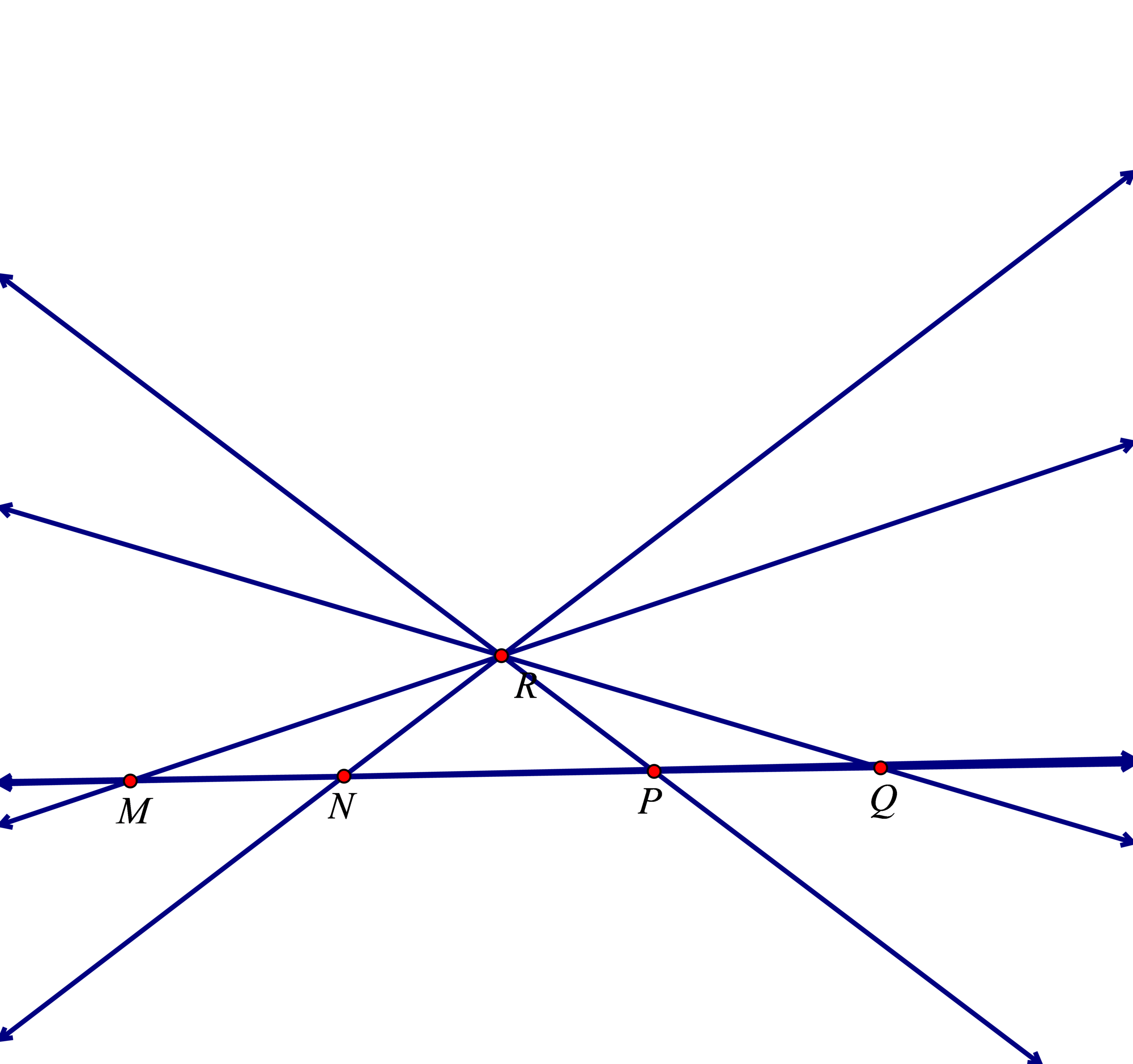
a) Có 5 đường thẳng, đó là đường thẳng MQ, RM, RN, RP, RQ.
b) Các tia gốc P là: PM, PN, PQ, PR. Hai tia PM, PN trùng nhau. Hai tia PM, PQ đối nhau.
